Abstract
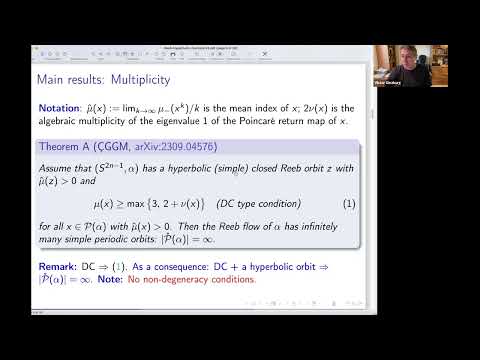
The presence of hyperbolic periodic orbits or invariant sets often has an affect on the global behavior of a dynamical system. In this talk we discuss two theorems along the lines of this phenomenon, extending some properties of Hamiltonian diffeomorphisms to dynamically convex Reeb flows on the sphere in all dimensions. The first one, complementing other multiplicity results for Reeb flows, is that the existence of a hyperbolic periodic orbit forces the flow to have infinitely many periodic orbits. This result can be thought of as a step towards Franks’ theorem for Reeb flows. The second result is a contact analogue of the higher-dimensional Le Calvez-Yoccoz theorem proved by the speaker and Gurel and asserting that no periodic orbit of a Hamiltonian pseudo-rotation is locally maximal. The talk is based on a joint work with Erman Cineli, Basak Gurel and Marco Mazzucchelli.