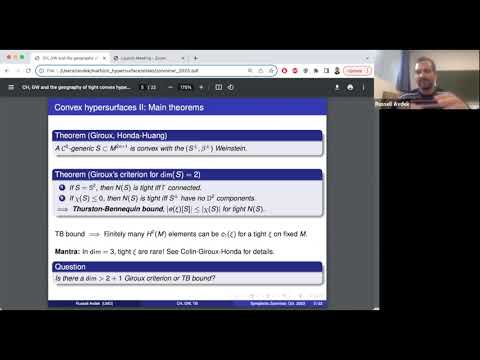
While convex hypersurfaces are well understood in 3d contact topology, we are just starting to explore their basic properties in high dimensions. I will describe how to compute contact homologies (CH) of their neighborhoods, which can be used to infer tightness in any dimension. Then I’ll give a general construction of high-dimensional convex hypersurfaces in the style of Gompf’s fiber sum. For these convex hypersurfaces, relative Gromov-Witten can often compute CH in the style of Diogo-Lisi. We’ll work through some interesting examples.