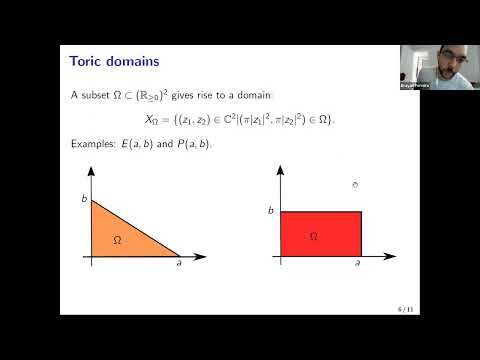
The question of whether a Symplectic manifold embeds into another is central in Symplectic topology. Since Gromov nonsqueezing theorem, it is known that this is a different problem from volume preserving embeddings. Symplectic capacities are invariants that give obstructions to symplectic embeddings. The first example of a symplectic capacity is given by the Gromov width, which measures the biggest ball that can be symplectically embedded into a symplectic manifold. In this talk, we are going to discuss the Gromov width for the example of disk cotangent bundles of spheres of revolution. The main results are for the Zoll cases and for the case of ellipsoids of revolution. The main tools are action angle coordinates (Arnold-Liouville theorem) and ECH capacities. This is joint work with Alejandro Vicente and Vinicius Ramos.