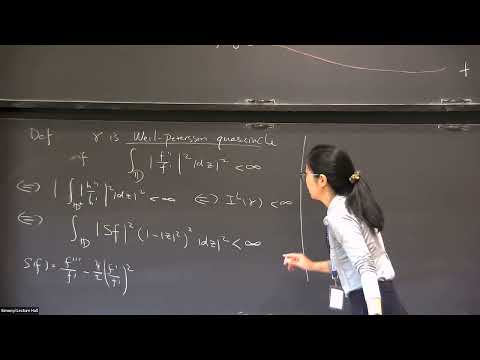The Loewner energy is a Möbius invariant quantity that measures the roundness of Jordan curves on the Riemann sphere. It arises from large deviation deviations of SLE0+ and is also a Kähler potential on the Weil-Petersson Teichmüller space. Motivated by AdS/CFT correspondence and the fact that Möbius transformations extend to isometries of the hyperbolic 3-space H3 , we look for quantities defined geometrically in H3 which equal the Loewner energy of a curve in the conformal boundary. We show that the Loewner energy equals the renormalized volume of a submanifold of H3 constructed using the Epstein surfaces associated to the hyperbolic metric on both sides of the curve. This is a work in progress with Martin Bridgeman (Boston College), Ken Bromberg (Utah), and Franco Vargas-Pallete (Yale).