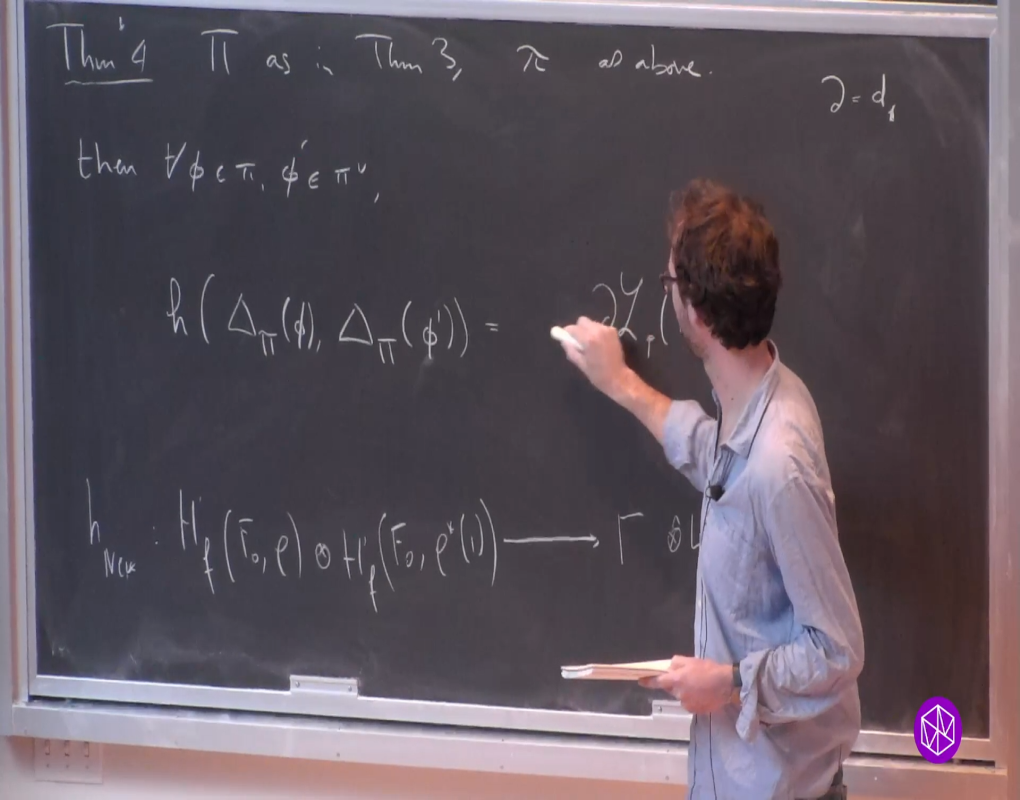Certain Rankin-Selberg motives of rank n(n+1) are endowed with algebraic cycles arising from maps of unitary Shimura varieties. Gan-Gross-Prasad conjectured that these cycles are analogous to Heegner points, in the sense that their nontriviality should be detected by derivatives of L-functions. I will propose another nontriviality criterion, based on p-adic L-functions. Under some assumptions, this variant can be established in a refined quantitative form, via a comparison of p-adic relative-trace formulas. Together with the recent LTXZZ Euler system, this gives cases of the p-adic Beilinson-Bloch-Kato conjecture of Perrin-Riou. (Joint work with Wei Zhang.)