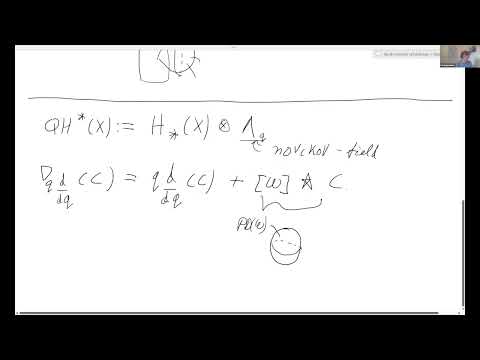Enumerative mirror symmetry is a correspondence between closed Gromov-Witten invariants of a space X, and period integrals of a family Y. One of the predictions of Homological Mirror Symmetry is that the closed Gromov-Witten invariants can be obtained from the Fukaya category. For Calabi-Yau varieties this has been demonstrated by Ganatra-Perutz-Sheridan. Recently, enumerative mirror symmetry has been extended, by including open Gromov-Witten invariants and extended period integrals. It is natural to expect that open Gromov-Witten invariants can be obtained from the Fukaya category. In this talk I will outline a construction which will demonstrate this for certain open Gromov-Witten invariants.