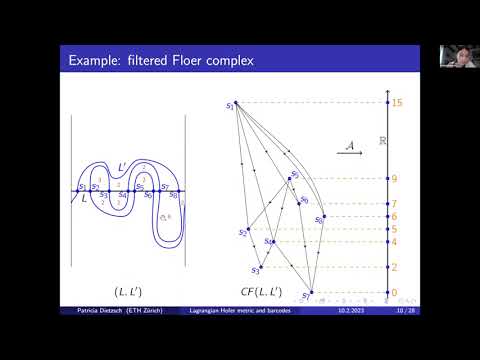
Filtered Lagrangian Floer homology gives rise to a barcode associated to a pair of Lagrangians.  It is well-known that the lengths of the finite bars and the spectral distance are lower bounds of the Lagrangian Hofer metric. In this talk we are interested in a reverse inequality.  I will explain an upper bound of the Lagrangian Hofer distance between equators in the cylinder in terms of a weighted sum of the lengths of the finite bars and the spectral distance.