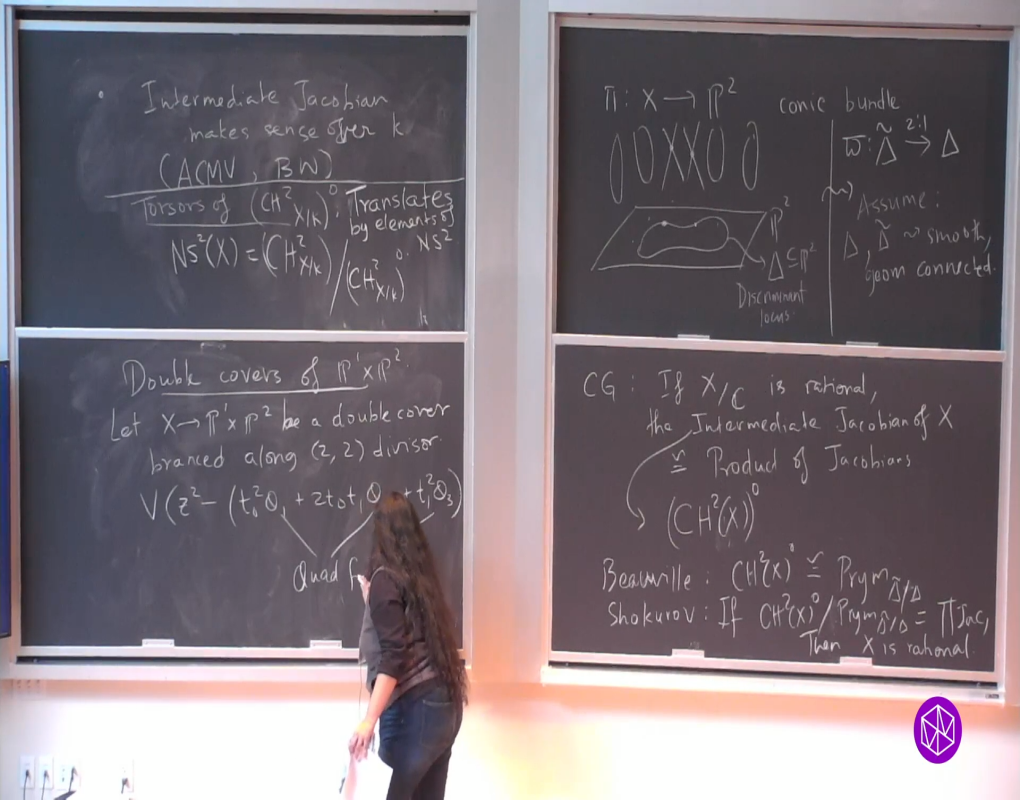Conic bundles are a geometrically rich class of varieties. Beauville showed that over an algebraically closed field, the group of algebraically trivial curve classes on a conic bundle threefold is isomorphic to the Prym variety of a double cover naturally associated with it. In joint work with Sarah Frei, Lena Ji, Bianca Viray and Isabel Vogt, we study curve classes on certain conic bundle threefolds over arbitrary fields of odd characteristic. We then use the description of these classes to study the rationality of such varieties. We study the intermediate Jacobian obstruction to rationality introduced by Hassett-Tschinkel and Benoist-Wittenberg, which is closely related to the structure of the space of curve classes on threefolds, and show that this obstruction is insufficient to characterize rationality.