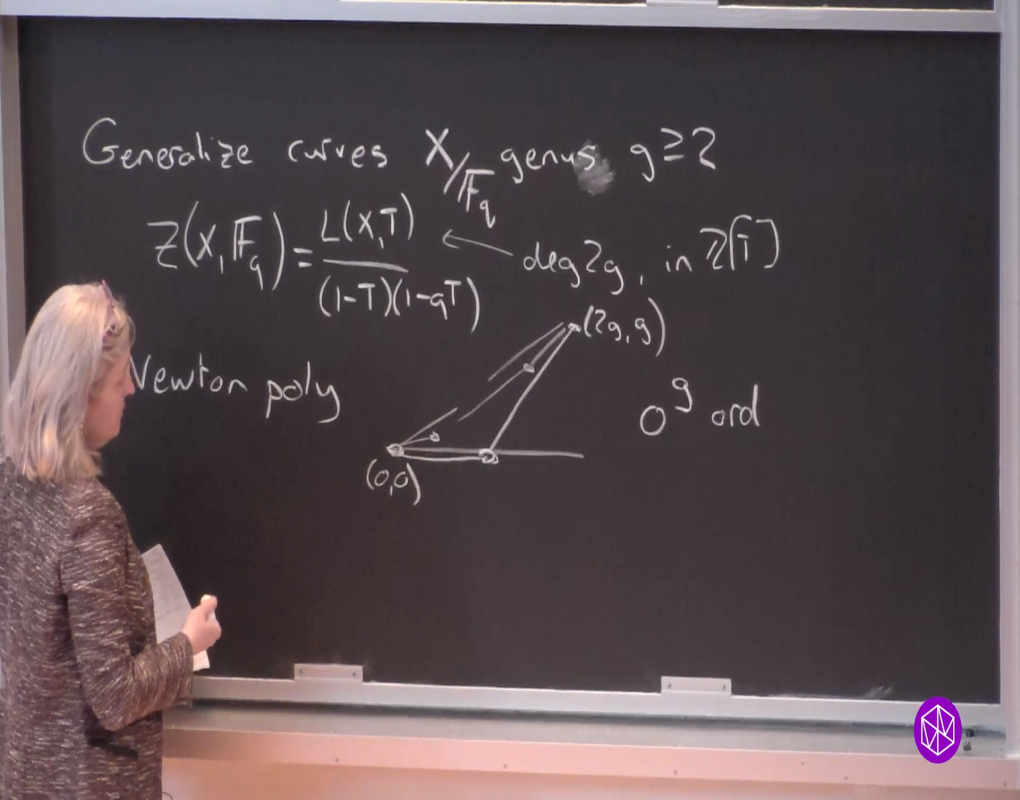The main topic of this talk is how the L-polynomials of abelian varieties vary, where we either fix a prime and vary the abelian variety, or fix the abelian variety and vary the prime. This L-polynomial determines the p-adic valuations of the normalized Weil numbers of the Frobenius morphism. I will start by discussing the case of elliptic curves, where the main distinction is whether the elliptic curve is ordinary or supersingular. Then we will switch to the case of curves that are cyclic covers of the projective line; the moduli spaces of these cyclic covers can be mapped to unitary Shimura varieties by the Torelli morphism. I will describe joint work with Li, Mantovan, and Tang, where we used this connection to obtain new results about L-polynomials of curves. First, for a fixed prime p, we prove cases of a conjecture of Oort for abelian varieties of arbitrarily large dimension. Second, for certain abelian varieties of dimension 4, we generalize a result of Elkies about infinitely many primes of non-ordinary reduction. Joint work with Li, Mantovan, Tang