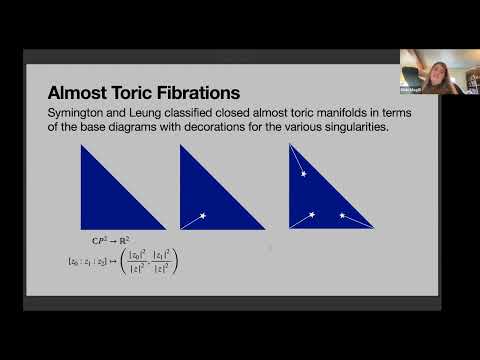
The ellipsoidal embedding function of a symplectic four manifold M measures how much the symplectic form on M must be dilated in order for it to admit an embedded ellipsoid of some eccentricity. It generalizes the Gromov width and ball packing numbers. In most cases, finitely many obstructions besides the volume determine the function. If there are infinitely many obstructions determining the function, M is said to have an infinite staircase. This talk will give a classification of which Hirzebruch surfaces have infinite staircases. We will focus on explaining the correspondence between the obstructions coming from exceptional classes and the constructions from almost toric fibrations. We define a way to mutate triples of exceptional classes to produce new triples of exceptional classes, which corresponds to mutations in almost toric fibrations. This is based on various joint work with Dusa McDuff, Ana Rita Pires, and Morgan Weiler.