Approximation of Generating Function Barcode for Hamiltonian Diffeomorphisms
Presenter
October 28, 2022
Abstract
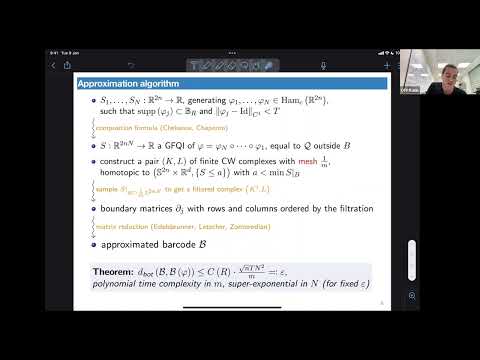
Persistence modules and barcodes are used in symplectic topology to define new invariants of Hamiltonian diffeomorphisms, however methods that explicitly calculate these barcodes are often unclear. In this talk I will define one such invariant called the GF-barcode of compactly supported Hamiltonian diffeomorphisms of R2n by applying Morse theory to generating functions quadratic at infinity associated to such Hamiltonian diffeomorphisms and provide an algorithm (i.e a finite sequence of explicit calculation steps) that approximates it along with a few computation examples. This is joint work with Pazit Haim-Kislev.