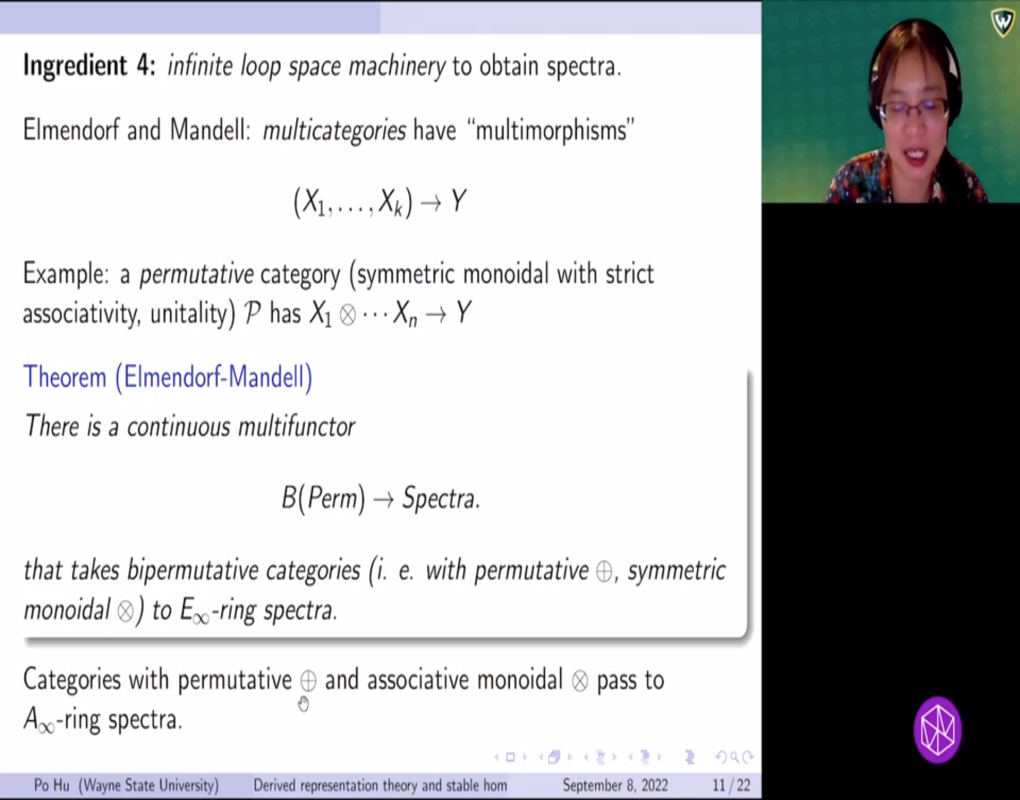
In recent years, the idea of categorification has become an important direction in topology. A primary example of categorification from knot theory is Khovanov homology, which categorifies the Jones polynomial, and is closely connected to many other link invariants including knot Floer homology. Generalizations of the Jones polynomial and of Khovanov homology, in turn, are intrinsically connected to the representation theory of sl_k. In this talk, I will discuss methods for constructing analogues of basic notions from Lie representation theory in the world of spectra. As an application, I will discuss the construction of a sl_k-homotopy type, categorifying the sl_k link invariants in the context of stable homotopy theory.