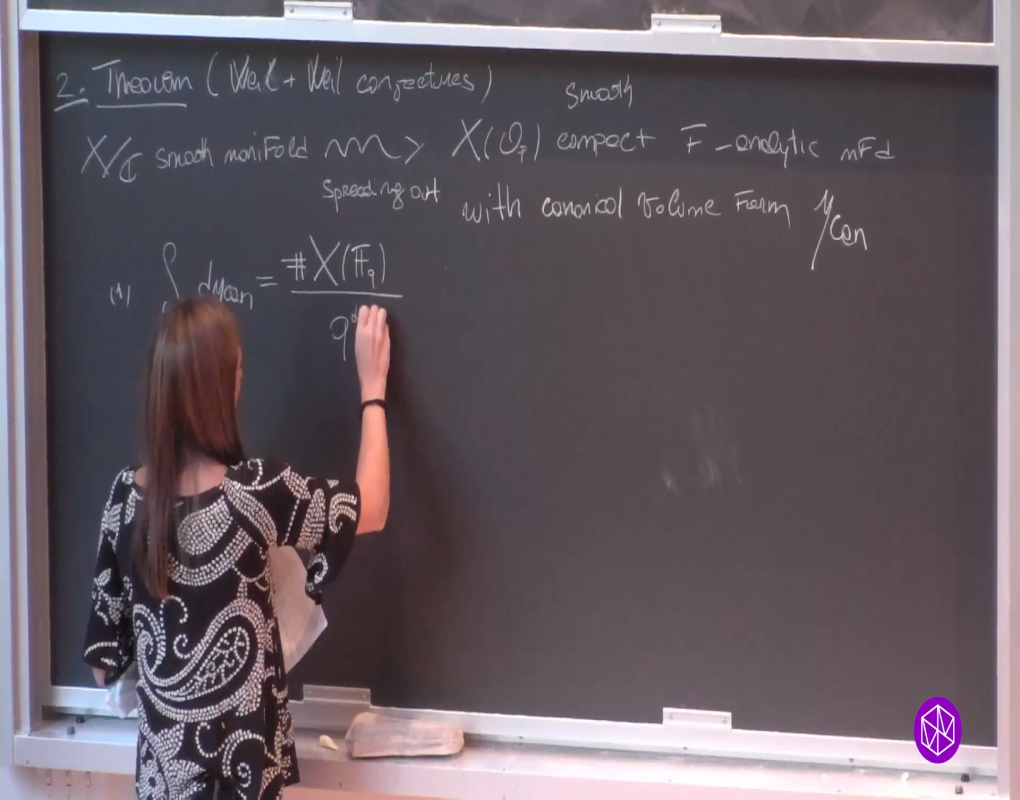Moduli spaces of (meromorphic) Higgs bundles and moduli spaces of one dimensional sheaves on surfaces with positive (or trivial) anti-canonical bundle can be interpreted as moduli of stable sheaves on non compact CY3 varieties. From this prospective, the so called BPS invariants for these moduli spaces have an interpretation in terms of curve counting on the CY3. This in turn imply that certain relations among the BPS invariants are to be expected. Extending the framework of Batyrev’s Theorem, we work over a non Archimedean field F and define a natural measure on the F-points of such moduli spaces. We then prove that the integral of a naturally defined function on the moduli space (with respect to the constructed measure) is independent of the Euler characteristic. This independence is the expected property for BPS invariants. This is a joint work with Giulio Orecchia and Dimitri Wyss.