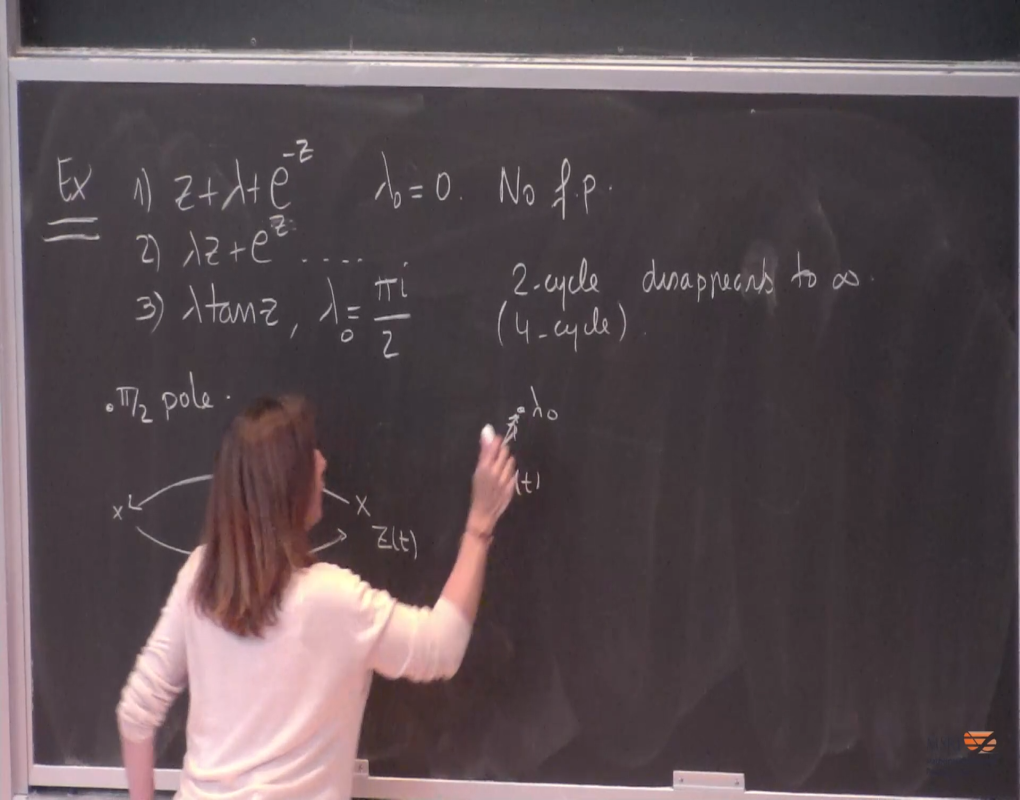In this talk we will discuss parameter spaces of natural families of transcendental meromorphic maps of finite type, parametrized over a complex manifold. In this setting, a new type of bifurcation arises for which a periodic cycle can disappear to infinity along a parameter curve. We shall relate these type of bifurcation parameters, with those for which an asymptotic value is a prepole (virtual cycle parameters), and use these relations to study stability of Julia sets ($J$-stability), concluding that $J-$stable parameters form an open and dense subset of the parameter space. All our theorems hold for general finite type maps in the sense of Epstein, satisfying certain conditions. This is joint work with Anna Miriam Benini and Matthieu Astorg.