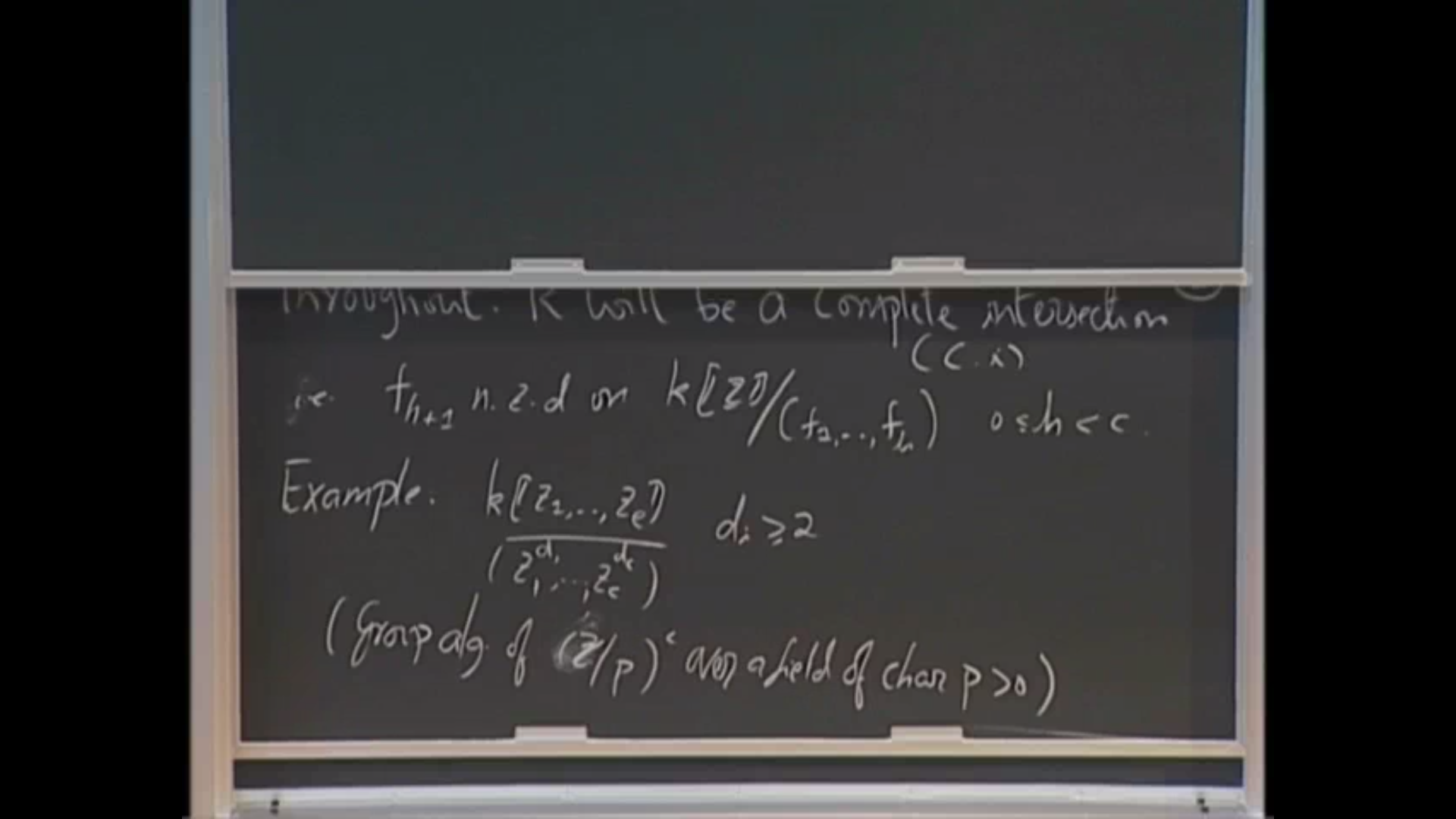The derived category of a complete intersection ring
Presenter
February 12, 2013
Keywords:
- complete intersections
- bounded derived category
- chain complexes
- thick subcategories
- noncommutative algebra
- representation theory
- homological algebra
- commutative algebra
- resolutions of modules
MSC:
- 18G35
- 18G10
- 18Gxx
- 18-xx
- 16Gxx
- 18E30
- 18Exx
Abstract
The aim of this talk is to explain how the bounded derived category of a complete intersection ring R is closely linked to the derived category of differential graded modules over a polynomial sub-algebra of the cohomology algebra of R. And how this has led to the discovery of new results on R-modules (estimates on numerical invariants, for one) as well as on the structural properties of the derived category itself (for instance, a classification of its thick subcategories) by passage to the polynomial ring. The presentation will be based on joint work, spread over many articles, with various subsets of the following collaborators: Lucho Avramov, Dave Benson, Ragnar-Olaf Buchweitz, Jon Carlson, Henning Krause, and Claudia Miller.