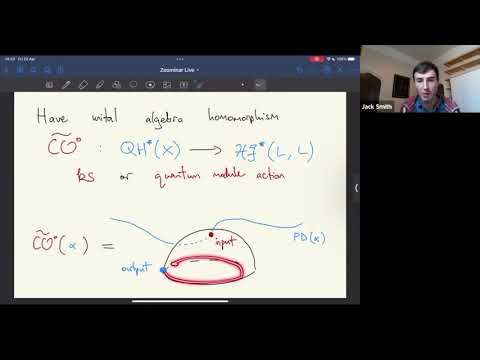
The Hochschild cohomology of the Floer algebra of a Lagrangian L, and the associated closed-open string map, play an important role in the generation criterion for the Fukaya category and in deformation theory approaches to mirror symmetry. I will explain how, in the monotone setting, one can build a map from the Floer cohomology of L with certain local coefficients to (a version of) Hochschild cohomology. This map makes things much more geometric, by transferring the algebraic complexity to the world of matrix factorisations, and is an isomorphism when L is a torus.