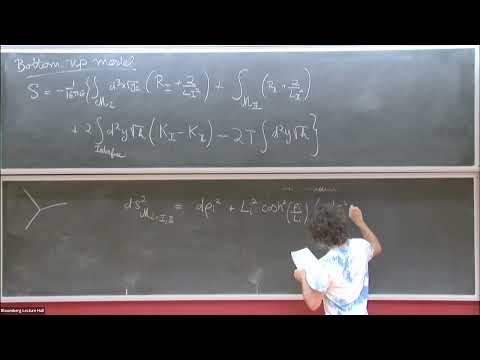Quantum extremal surfaces and islands have led us to rethink the very meaning of microscopic entropy in the presence of dynamical gravity. I will present some work elucidating how the island/QES prescription emerges in a simple doubly holographic setup where we have analytic control. We will consider two holographic 2d CFTs joined at an interface  such that the bulk dual is a geometry that interpolates between two locally 3d AdS geometries with different AdS lengths. In particular we will consider systems where the transition region is a thin brane with tension T. In the limit of large tension, the brane gets pushed outward towards the boundary, meaning the effective theory on the brane is conformal and gravity almost decouples. We show precisely how the canonical CFT entropy and the remaining gravity dynamics leads to an island formula in this setup. The location of the island is identified with where the RT surface crosses the brane in the full holographic 3d picture.