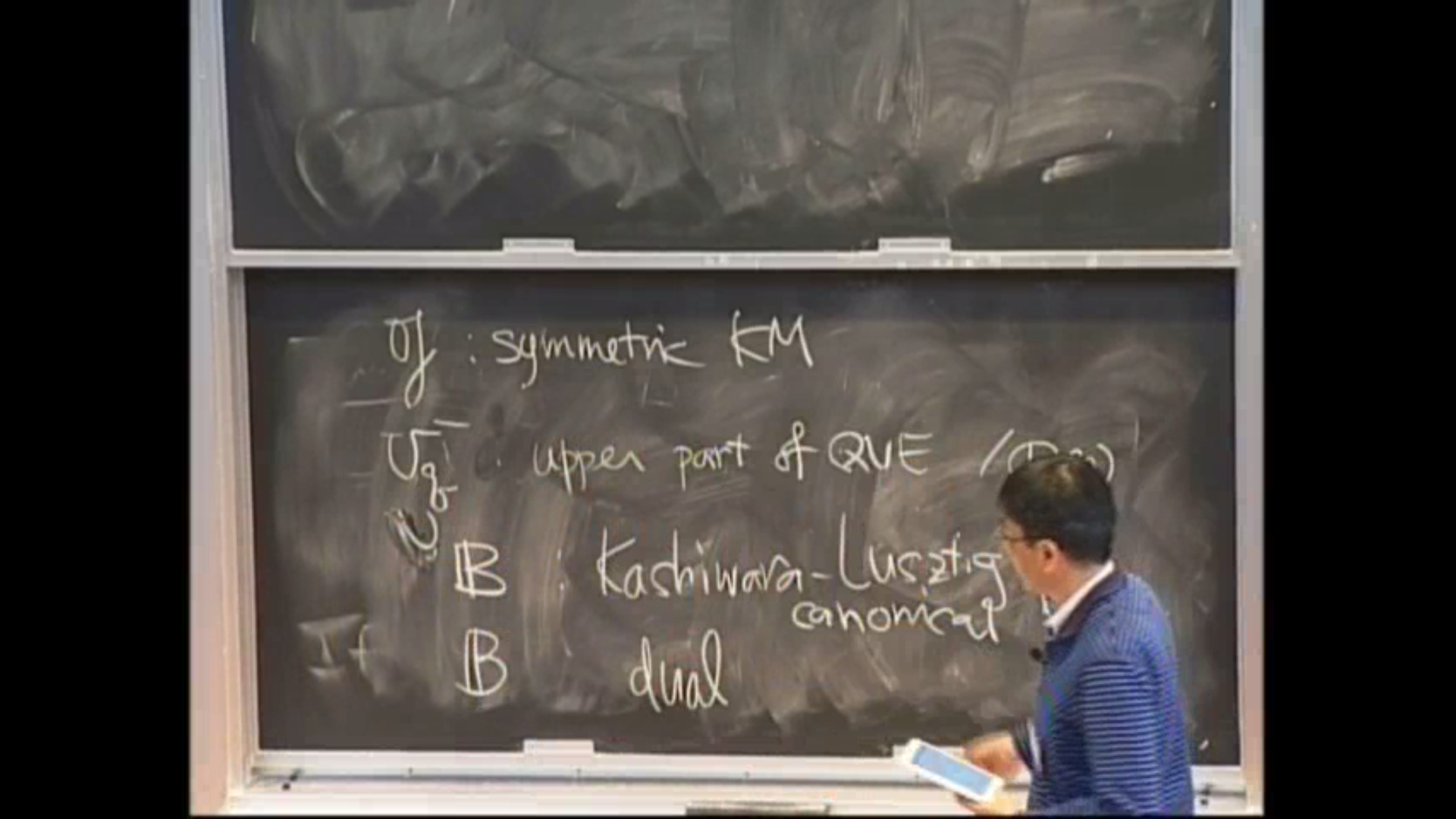Cluster algebras and singular supports of perverse sheaves
Presenter
April 9, 2013
Keywords:
- perverse sheaves
- canonical bases
- unipotent subgroups
- cluster algebra
- quantum cluster algebra
- noncommutative algebra
- noncommutative algebraic geometry
- module theory
- ring theory
- representation theory
- D-modules
- deformation quantization
MSC:
- 13F60
- 16G20
- 16Gxx
- 14Fxx
- 14-xx
- 81-xx
- 81Rxx
- 81R50
- 81R60
- 81Sxx
- 81S10
- 14Fxx
- 14F10
Abstract
We propose an approach via perverse sheaves on the space of quiver representations to Geiss-Leclerc-Schroer's conjecture on the (quantum) cluster algebra structure on the coordinate ring of a unipotent subgroup and the dual canonical base. The cluster algebra structure has been explained in the representation theory of the preprojective algebra. So the idea is to relate it to perverse sheaves via singular supports.