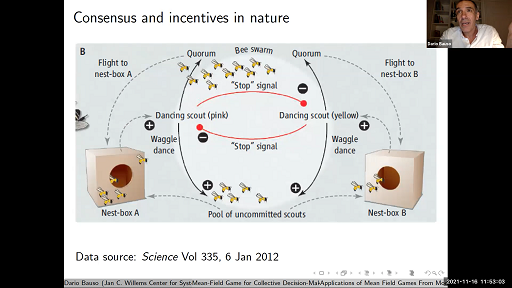
In this talk, we study the optimal control problem arising from the mean-field game formulation of the collective decision-making in honeybee swarms. A population of homogeneous players (the honeybees) has to reach consensus on one of two options. We consider three states: the first two represent the available options (or strategies), and the third one represents the uncommitted state. We formulate the continuous-time discrete-state mean-field game model. The contributions of this talk are the following: i) we propose an optimal control model where players have to control their transition rates to minimize a running cost and a terminal cost, in the presence of an adversarial disturbance; ii) we develop a formulation of the micro-macro model in the form of an initial-terminal value problem (ITVP) with switched dynamics; iii) we study the existence of stationary solutions and the mean-field Nash equilibrium for the resulting switched system; iv) we show that under certain assumptions on the parameters, the game does not admit Nash equilibrium solutions but only periodic solutions; and v) we analyze the resulting microscopic dynamics in a structured environment where a finite number of players interact through a network topology.