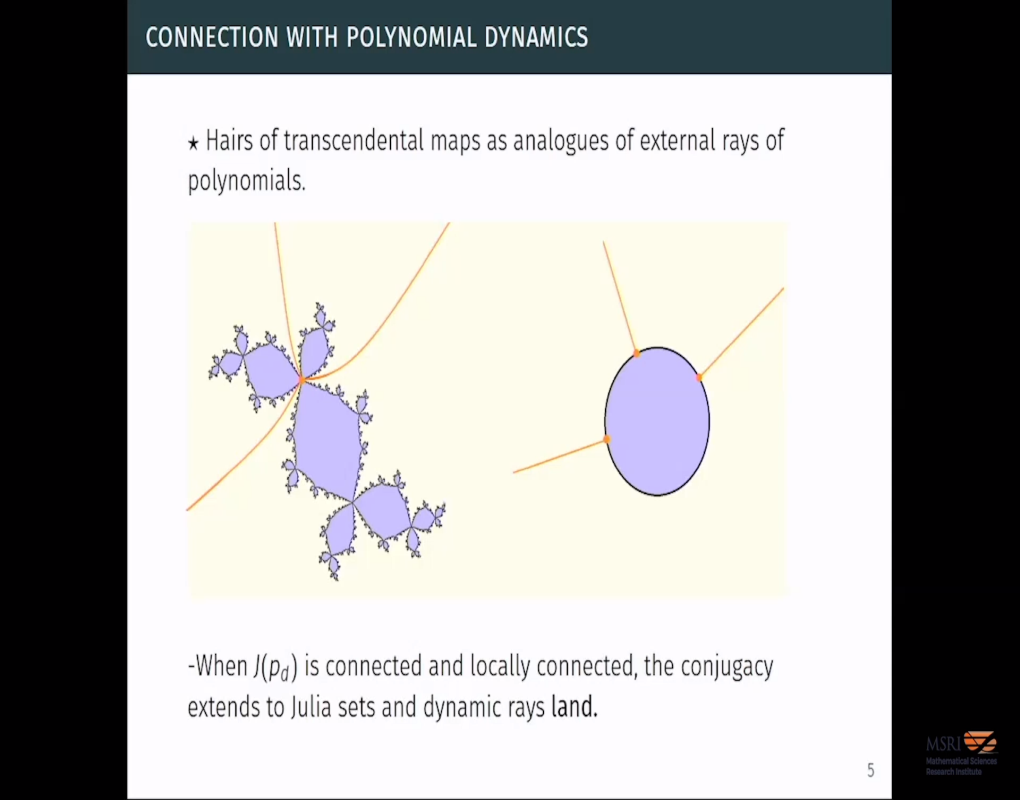
Transcendental Entire Functions with Cantor Bouquet Julia Sets
Presenter
February 4, 2022
Keywords:
- Transcendental entire function
- Cantor bouquet
- dynamic rays
- criniferous
- Eremenko-Lyubich class
MSC:
- 37F10
- 54H20
- 30D05
Abstract
In the study of the dynamics of a transcendental entire function f, we aim to describe its locus of chaotic behaviour, known as its Julia set and denoted by J(f). For many such f, the Julia set is a collection of unbounded curves that escape to infinity under iteration and form a Cantor bouquet, i.e., a subset of the complex plane ambiently homeomorphic to a straight brush. We show that there exists f whose Julia set J(f) is a collection of escaping curves, but J(f) is not a Cantor bouquet. On the other hand, we prove for certain f that if J(f) contains an absorbing Cantor bouquet, that is, a Cantor bouquet to which all escaping points are eventually mapped, then J(f) must be a Cantor bouquet. This is joint work with L. Rempe.