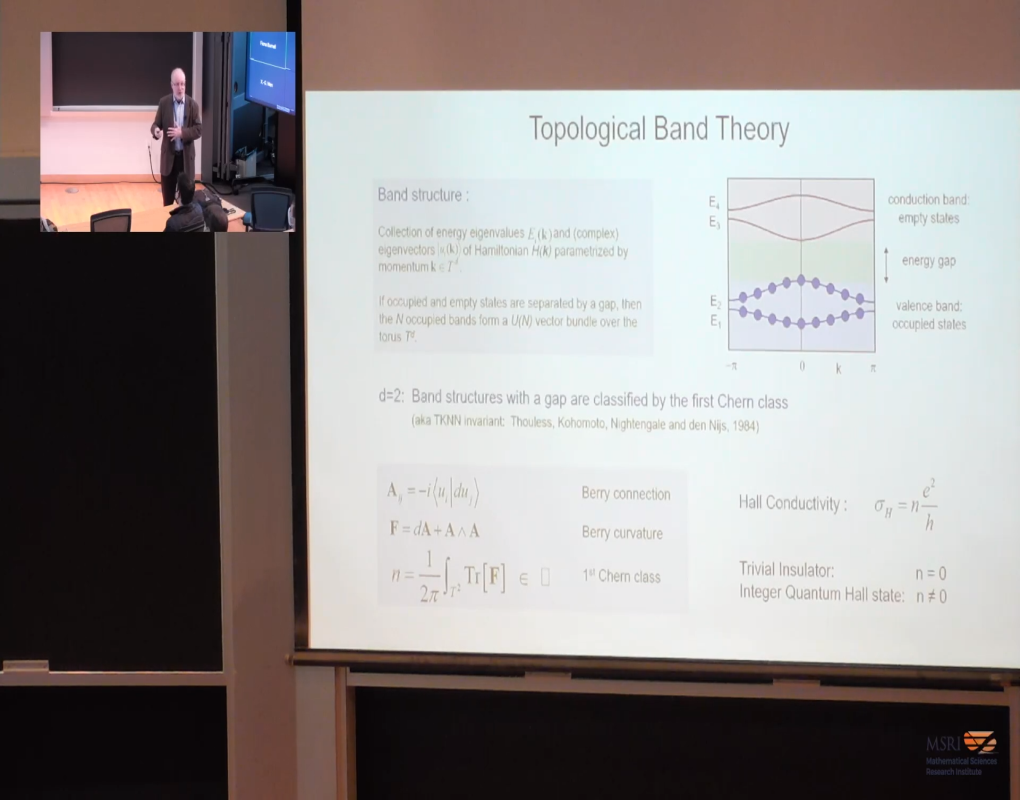
A dramatic consequence of the role of topology in the structure of quantum matter is the existence of topological invariants that are reflected in quantized response functions. In this talk we will discuss a new variant on this theme. We introduce a non-linear frequency dependent D+1 terminal conductance that characterizes a D dimensional Fermi gas, generalizing the Landauer conductance in D = 1. For a ballistic conductor we show that this conductance is quantized and probes the Euler characteristic of the Fermi sea. We critically address the roles of electrical contacts and of Fermi liquid interactions, and we propose experiments on 2D Dirac materials such as graphene using a triple point contact geometry. We show that the Euler characteristic provides a fundamental characterization of the long range quantum entanglement in a Fermi gas, analogous to the central charge, c, in D = 1.