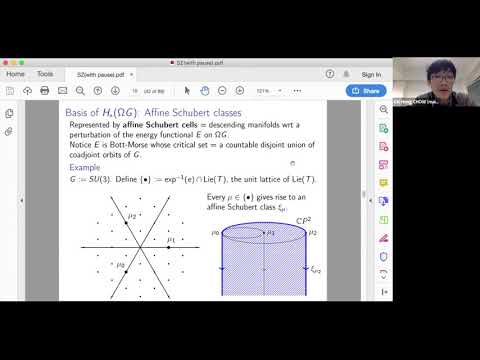
We will discuss a complete computation of Savelyev's homomorphism associated to any coadjoint orbit of a compact Lie group G, where the domain is restricted to the based loop homology of G. This gives at the same time some applications to the Hamiltonian groups of these spaces and a geometric proof of an unpublished theorem of Peterson. This theorem tells us explicitly how the multiplicative structure constants of the based loop homology of G determine those of the quantum cohomology of its coadjoint orbits.