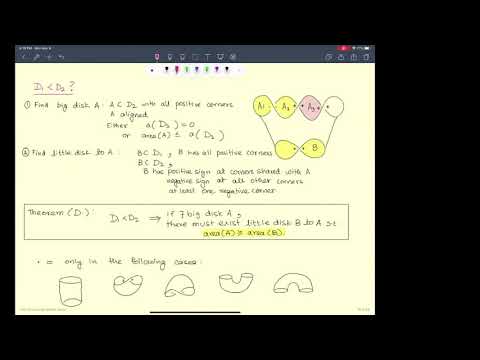
We present some obstructions to the existence of Lagrangian cobordisms in ℝ4. The obstructions arise from studying moduli spaces of holomorphic disks with corners with boundaries on immersed objects called Lagrangian tangles. The obstructions boil down to area relations and sign conditions on disks bound by knot diagrams of the boundaries of the Lagrangian. We present examples of pairs of knots that cannot be Lagrangian cobordant and knots that cannot bound Lagrangian disks.