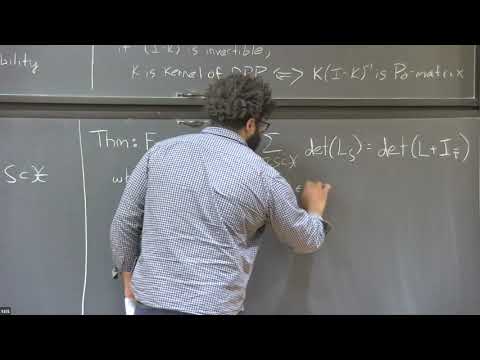A random point process is said to be determinantal if finite subset probabilities correspond to principal minors of some matrix. Determinantal point processes (DPPs) appear in a wide variety of settings, from random matrix theory to combinatorics, and recently have become of interest to the machine learning community. In this two-hour talk, I will give a brief introduction to DPPs, provide some well-known examples, and attempt to survey some of the key results and open questions.