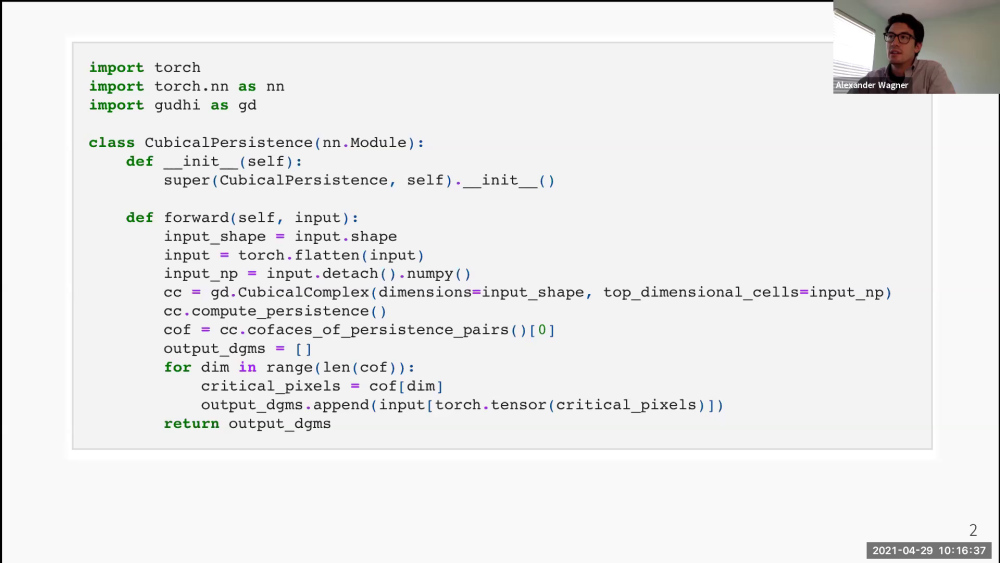
The computational cost of calculating the persistence diagram for a large input inhibits its use in a deep learning framework. The fragility of the persistence diagram to outliers and the instability of critical cells present further challenges. In this talk, I will present two distinct approaches to address these concerns. In the first approach, by replacing the original filtration with a stochastically downsampled filtration on a smaller complex, one can obtain results in topological optimization tasks that are empirically more robust and much faster to compute than their vanilla counterparts. In the second approach, we work with the set of persistence diagrams of subsets of a fixed size rather than with the diagram of the complete point cloud. The benefits of this distributed approach are a greater degree of practical robustness to outliers, faster computation due to parallelizability and scaling of the persistence algorithm, and an inverse stability theory. After outlining these benefits, I will describe a dimensionality reduction pipeline using distributed persistence. This is joint work with Elchanan Solomon and Paul Bendich.