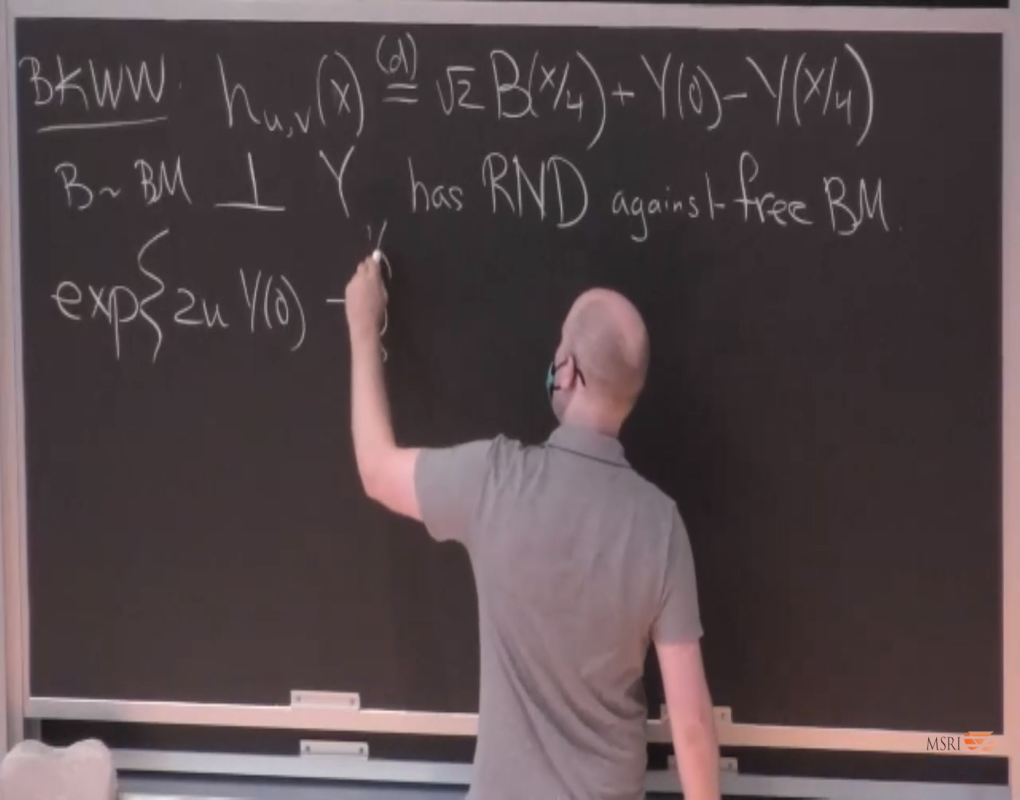Consider the KPZ equation on an spatial interval [0,1] with mixed Neumann boundary conditions at 0 and 1. For each given pairs of boundary parameters (u,v), there should exist a unique stationary measure for the height profile differences (i.e., for the derivative of the KPZ equation). In this talk I will describe recent work in which we show that for each pair (u,v) satisfying u+v>0, certain exponentially reweighted Brownian paths measures are stationary measures for the corresponding open KPZ equation. Along the way, we will also encounter the open ASEP, as well as Askey-Wilson processes and q-function asymptotics. This is mainly based on my recent work with Alisa Knizel, though also relies on earlier work with Hao Shen as well as earlier work of Wlodzimierz Bryc, Jacek Wesolowski and Yizao Wang. I will also touch on some recent related work of Wlodzimierz Bryc, Alexey Kuznetsov, Jacek Wesolowski and Yizao Wang; as well as work of Guillaume Barraquand and Pierre Le Doussal.