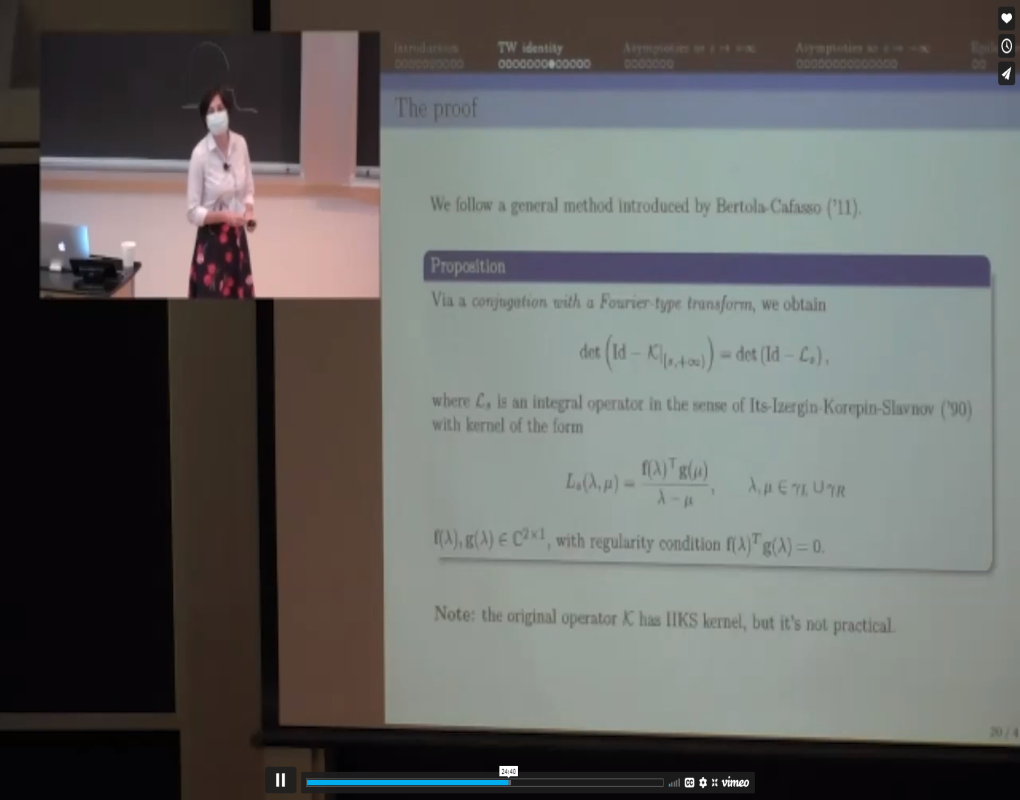
We study Fredholm determinants of a class of integral operators, whose kernels can be expressed as double contour integrals of a special type. Such Fredholm determinants appear in various random matrix and statistical physics models. We show that the logarithmic derivatives of the Fredholm determinants are directly related to solutions of the Painlevé II hierarchy. This confirms and generalizes a recent conjecture by Le Doussal, Majumdar, and Schehr (2018). In addition, we obtain asymptotics at infinity for the Painlevé transcendents and large gap asymptotics for the corresponding point processes. This is a joint work with Mattia Cafasso (Univ. Angers) and Tom Claeys (UC Louvain).