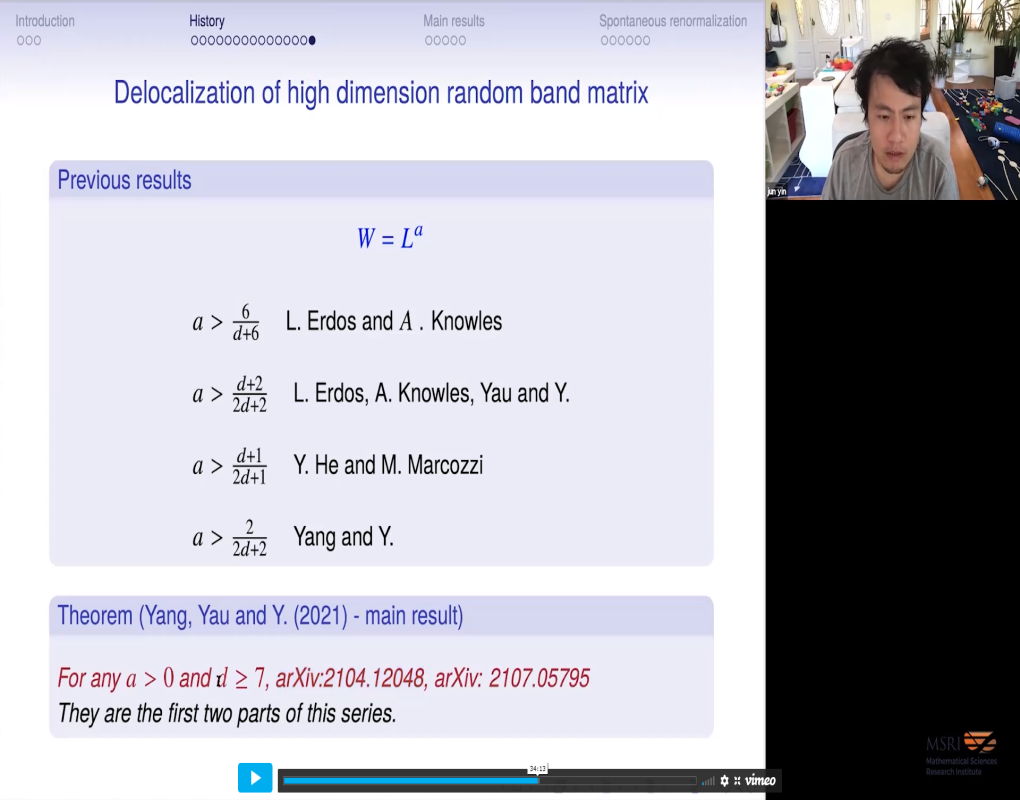
One famous conjecture in quantum chaos and random matrix theory is the so-called phase transition conjecture of random band matrices. It predicts that the eigenvectors' localization-delocalization transition occurs at some critical bandwidth $\mathrm{Wc}(\mathrm{d})$, which depends on the dimension $\mathrm{d}$. The well-known Anderson model and Anderson conjecture have a similar phenomenon. It is widely believed that $\mathrm{Wc}(\mathrm{d})$ matches $1 / \lambda \mathrm{c}(\mathrm{d})$ in the Anderson conjecture, where $\lambda \mathrm{c}(\mathrm{d})$ is the critical coupling constant. Furthermore, this random matrix eigenvector phase transition coincides with the local eigenvalue statistics phase transition, which matches the Bohigas-Giannoni-Schmit conjecture in quantum chaos theory. We proved the eigenvector's delocalization property for most of the general $d>=8$ random band matrix as long as the size of this random matrix does not grow faster than its bandwidth polynomially. In other words, as long as bandwidth $W$ is larger than $L^ \epislon$ for some $epislon $>0$. It is joint work with H.T. Yau (Harvard) and F. Yang (Upenn).