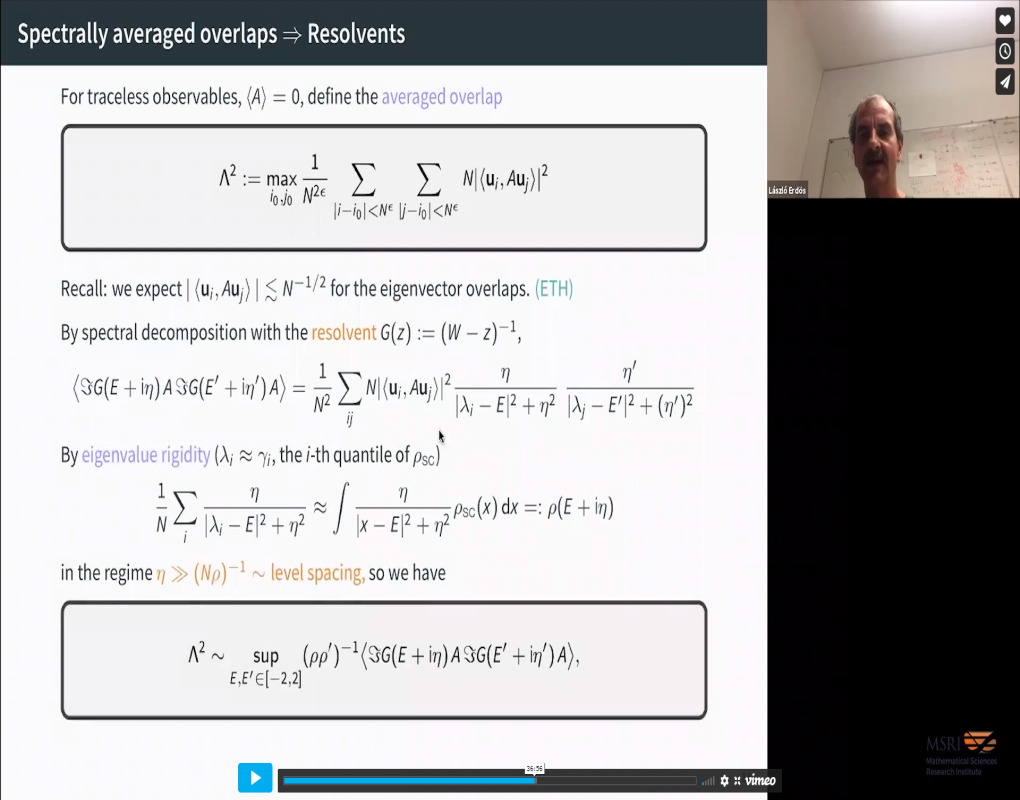
We prove that any deterministic matrix is approximately the identity in the eigenbasis of a large random Wigner matrix W with an optimal error inversely proportional to the square root of the dimension. This verifies a strong form of Quantum Unique Ergodicity with an optimal convergence rate and we also prove Gaussian fluctuations around this convergence. The key technical tool is a new multi-resolvent local law for Wigner ensemble and the Dyson Brownian motion for eigenvector overlaps.