Hyperbolic geometry in biological networks
Presenter
May 5, 2021
Keywords:
- olfaction
- Simplicial Complexes
MSC:
- 92F99
- 55U10
Abstract
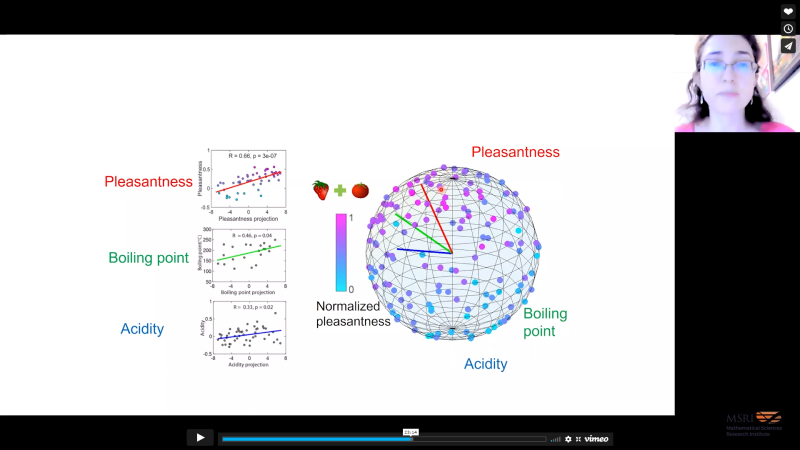
Using the sense of smell as an example, I will describe both theoretical reasons and experimental evidence that natural stimuli and human perception can be mapped onto a low dimensional curved surface. This surface turns out to have a negative curvature, corresponding to a hyperbolic metric. Although this map was derived purely from the statistics of co-occurrence between mono-molecular odorants in the natural environment it revealed topography in the organization of human perception of smell. I will conclude with arguments for why hyperbolic metric can be useful for other sensory systems.