Topological insights on neuronal morphologies
Presenter
May 4, 2021
MSC:
- 55N99
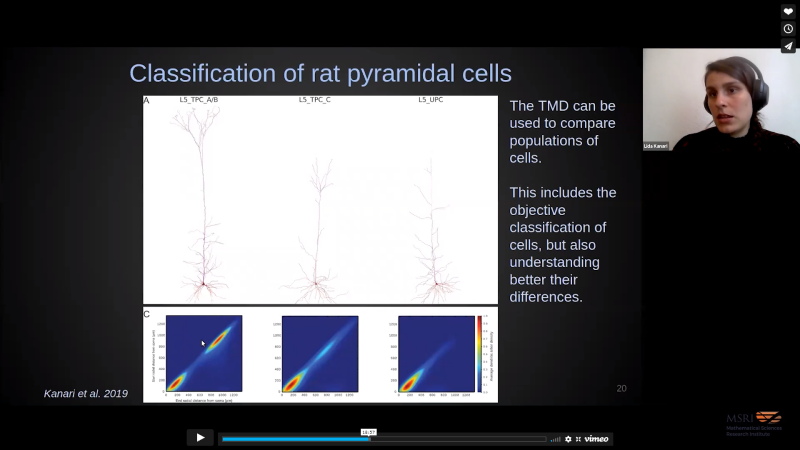
Abstract
The morphological diversity of neurons supports the complex information-processing capabilities of biological neuronal networks. A major challenge in neuroscience has been to reliably describe neuronal shapes with universal morphometrics that generalize across cell types and species. Inspired by algebraic topology, we have developed a topological descriptor of trees that couples the topology of their complex arborization with their geometric structure, retaining more information than traditional morphometrics. The topological morphology descriptor (TMD) has proved to be very powerful in separating neurons into well-defined groups on morphological grounds. The TMD algorithm led to the discovery of two distinct morphological classes of pyramidal cells in the human cortex that also have distinct functional roles, suggesting the existence of a direct link between the anatomy and the function of neurons. The TMD-based classification also led to the objective and robust morphological clustering of rodent cortical neurons. Recently we proved that the TMD of neuronal morphologies is also essential for the computational generation (i.e., synthesis) of dendritic morphologies. Our results demonstrate that a topology-based synthesis algorithm can reproduce both morphological and electrical properties of reconstructed biological rodent cortical dendrites and generalizes well to a wide variety of different dendritic shapes. Therefore it is suitable for the generation of unique neuronal morphologies to populate the digital reconstruction of large-scale, physiologically realistic networks.