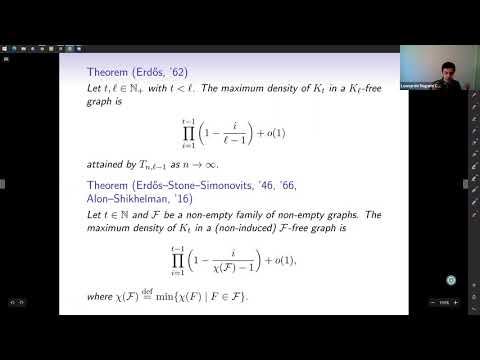
What edge density of a graph guarantees that that it will contain a particular subgraph? Or one of a given family F of subgraphs? The celebrated Erdős--Stone--Simonovits Theorem characterizes the maximum edge density in F-free graphs, in terms of the minimum {\em chromatic number} of any graph in the family F. More recently, generalizations of this theorem for ordered graphs, cyclically ordered graphs, edge-ordered graphs, etc. were shown in terms of appropriately defined chromatic numbers. In a recent joint work with A. Razborov, we proved an analogue of this theorem in the general setting of "graphs with an arbitrary extra structure" (formally, these are encoded by an open interpretation from the theory of graphs to some universal first-order theory TT) in terms of an {\em abstract chromatic number}. However, as its name suggests, the initial formula for this abstract chromatic number is so abstract that its computability was left as an open question. In this talk, I will present this generalization of the Erdős--Stone--Simonovits Theorem, and an alternative formula for the abstract chromatic number based on a partite version of Ramsey's Theorem. This implies the computability of the abstract chromatic number when the underlying universal first-order theory TT is finitely axiomatizable. This lecture will require no special background knowledge.