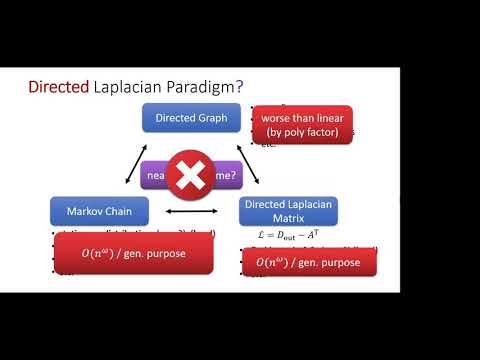
This talk introduces a directed analog of the classical Laplacian matrix and discusses algorithms for solving certain problems related to them. Of particular interest is that using such algorithms, one can compute the stationary distribution of a Markov chain to high accuracy with a number of arithmetic operations close to the number of possible transitions. The analogous problem in the low space setting, in contrast, remains open.