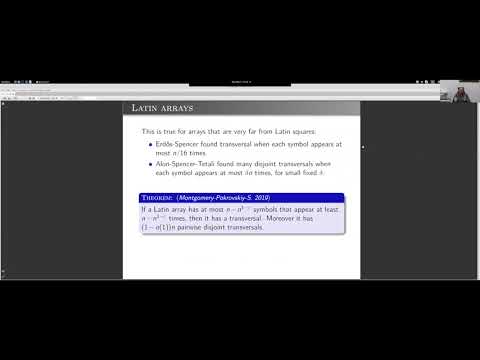
A subgraph of an edge-coloured graph is called rainbow if all its edges have distinct colours.  The study of rainbow subgraphs goes back to the work of Euler on Latin squares in the 18th century.  Since then rainbow structures were the focus of extensive research and found numerous applications in design theory and graph decompositions. In this talk we discuss how probabilistic reasoning can be used to attack several old problems in this area, leading to substantial progress on several well-known conjectures of Ryser, Brouwer, Ringel, and Graham-Sloane.   Based on joint works with Keevash, Montgomery, Pokrovskiy and Yepremian.