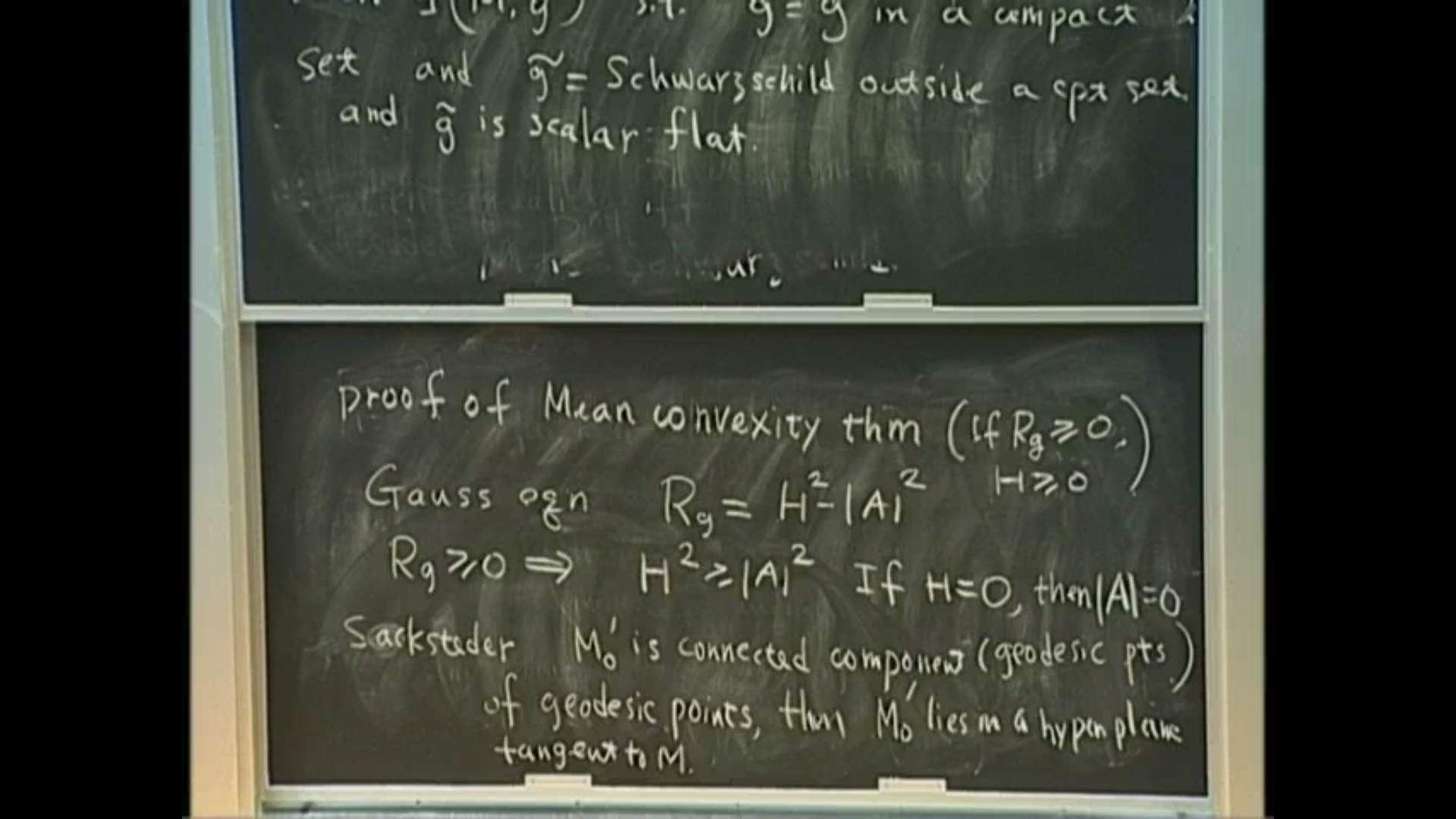Since the time of Gauss, geometers have been interested in the interplay between the intrinsic structure of hypersurfaces and their extrinsic geometry from the ambient space. Many classical results discuss the sectional curvature. For example, it is known that a complete hypersurface in Euclidean space with non-negative sectional curvature is either convex or a generalized hypercylinder. In a series of joint work with Damin Wu, we study hypersurfaces with non-negative scalar curvature. We prove that a closed hypersurface with nonnegative scalar curvature must be weakly mean convex. In general, vanishing scalar curvature causes analytical difficulties because the scalar curvature operator may not be elliptic. We tackle the problem by studying the level sets of a height function, which is motivated by general relativity. We further extend our proof to unbounded hypersurfaces which are asymptotically flat at infinity and obtain applications in the positive mass theorem and the Penrose inequality.