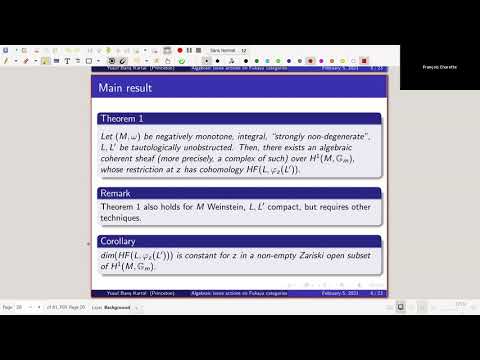
The purpose of this talk is to explore how Lagrangian Floer homology groups change under (non-Hamiltonian) symplectic isotopies on a (negatively) monotone symplectic manifold (M,ω)(M,ω) satisfying a strong non-degeneracy condition. More precisely, given two Lagrangian branes L,L′L,L′, consider family of Floer homology groups HF(ϕv(L),L′)HF(ϕv(L),L′), where v∈H1(M,ℝ)v∈H1(M,R) and ϕvϕv is the time-1 map of a symplectic isotopy with flux vv. We show how to fit this collection into an algebraic sheaf over the algebraic torus H1(M,𝔾m)H1(M,Gm). The main tool is the construction of an "algebraic action" of H1(M,𝔾m)H1(M,Gm) on the Fukaya category. As an application, we deduce the change in Floer homology groups satisfy various tameness properties, for instance, the dimension is constant outside an algebraic subset of H1(M,𝔾m)H1(M,Gm). Similarly, given closed 11-form αα, which generates a symplectic isotopy denoted by ϕtαϕαt, the Floer homology groups HF(ϕtα(L),L′)HF(ϕαt(L),L′) have rank that is constant in tt, with finitely many possible exceptions.