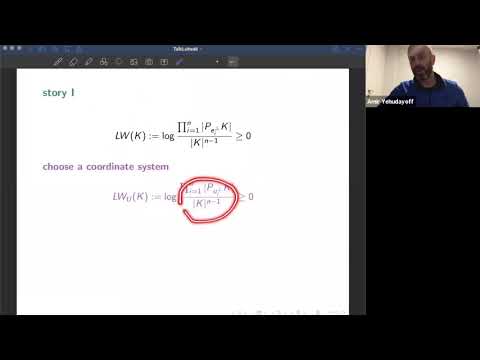
What can we say on a convex body from seeing its projections? In the 80s, Lutwak introduced a collection of measurements that capture this question. He called them the affine quermassintegrals. They are affine invariant analogues of the classical quermassintegrals (a.k.a. intrinsic volumes) from the Brunn-Minkowski theory. Lutwak conjectured that among all convex bodies of a given volume, they are minimized precisely on ellipsoids. The known cases of this conjecture correspond to the Blaschke-Santalo and Petty projection inequalities. Petty's inequality, for example, is a strict generalization of the classical isoperimetric inequality. Our main result confirms Lutwak's conjecture, including a characterization of the equality cases, in a single unified framework. Among other things, we also prove that ellipsoids are the only local minimizers.