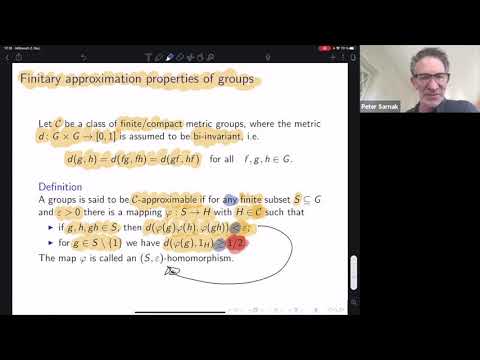
Several well-known open questions (such as: are all groups sofic/hyperlinear?) have a common form: can all groups be approximated by asymptotic homomorphisms into the symmetric groups Sym(n)Sym(n) (in the sofic case) or the finite dimensional unitary groups U(n)U(n) (in the hyperlinear case)? In the case of U(n)U(n), the question can be asked with respect to different metrics and norms. We answers, for the first time, one of these versions, showing that there exist fintely presented groups which are not approximated by U(n)U(n) with respect to the Frobenius nor. Our strategy is to show that some higher dimensional cohomology vanishing phenomena imply stability, that is, every Frobenius-approximate homomorphism into finite-dimensional unitary groups is close to an actual homomorphism. This is combined with existence results of certain non-residually finite central extensions of lattices in some simple pp-adic Lie groups. These groups act on high rank Bruhat-Tits buildings and satisfy the needed vanishing cohomology phenomenon and are thus stable and not Frobenius-approximated.