Abstract
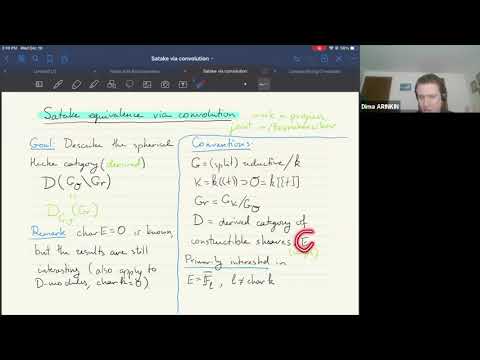
The talk is about convolution in the setting of geometric representation theory. What are its formal properties? As a starting point, let G be a group and let D(G) be the derived category of constructible sheaves on it. Convolution turns D(G) into a monoidal category, which is rigid (every object is dualizable) if and only if G is proper (this statement is due to Boyarchenko and Drinfeld).
In this talk, I develop the formalism of convolution using the language of derived algebraic geometry, and then apply these techniques to the (spherical) Hecke category and related objects.