Lecture slides available here: https://etale.site/writing/msri-K2.pdf Algebraic K-theory is an invariant of schemes, which measures them through their vector bundles. As proved by Blumberg--Gepner--Tabuada, when defined on stable ∞-categories it may be characterized as "the universal additive invariant". This gives rise to trace maps to other invariants such as topological Hochschild and cyclic homologies (THH and TC), which may be seen as analogs of the Chern character. I will explain this perspective, as well as an interpretation of the cyclotomic trace map to TC in terms of derived algebraic geometry which arises naturally from viewing THH as factorization homology over the circle. 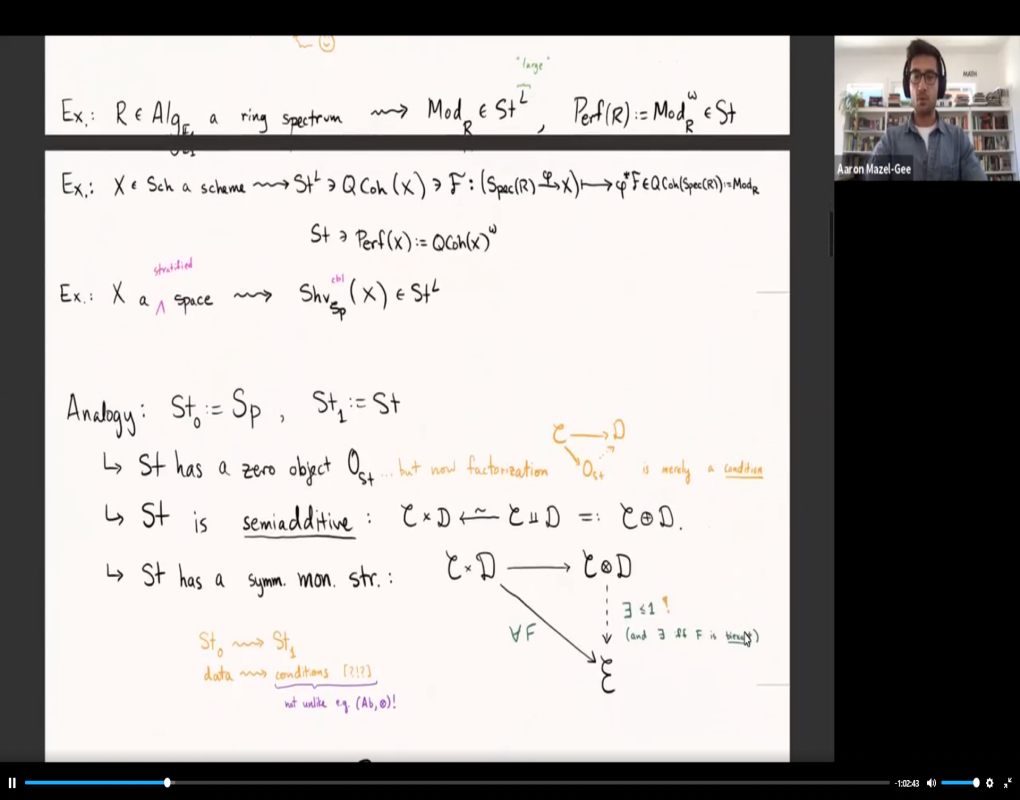Secondary algebraic K-theory is a categorification of algebraic K-theory, which measures schemes through their sheaves of categories. It is inspired by elliptic cohomology and the chromatic redshift conjecture; it is closely related to the Brauer group and to the K-theory of varieties. As proved in forthcoming work, when defined on stable (∞,2)-categories it may be characterized as "the universal 2-additive invariant". I will explain what this means, and speculate on the resulting 2-dimensional trace maps to higher-dimensional forms of factorization homology and TC (inspired by Carlsson--Douglas--Dundas). In particular, I will discuss the notion of a stable (∞,2)-category, and highlight a number of intriguing patterns that emerge as one moves up and down the categorical ladder. This represents joint work with David Ayala, Nick Rozenblyum, and Reuben Stern.