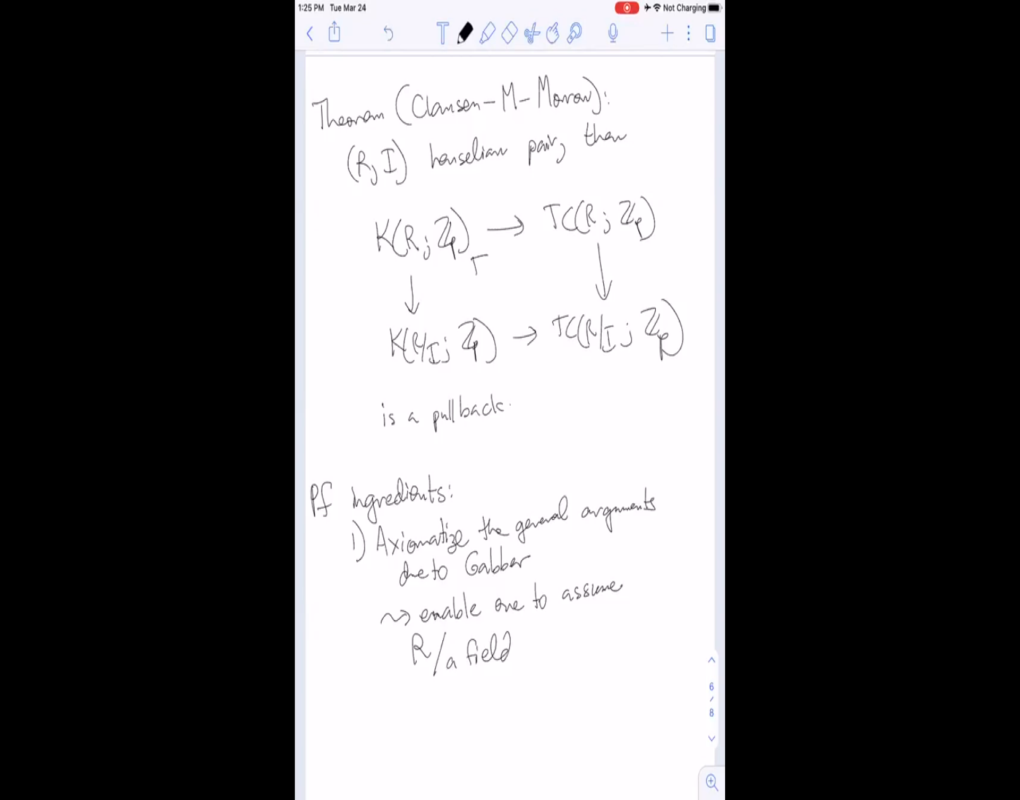
The cyclotomic trace from algebraic K-theory to topological cyclic homology is an important computational tool because of the Dundas-Goodwillie-McCarthy theorem, which states that the trace induces an isomorphism of relative theories with respect to nilpotent ideals. After p-adic completion, this result can be strengthened to henselian pairs, generalizing also the Gabber-Suslin rigidity theorem in the l-adic context. I will explain this generalization and some consequences. Joint with Dustin Clausen and Matthew Morrow.