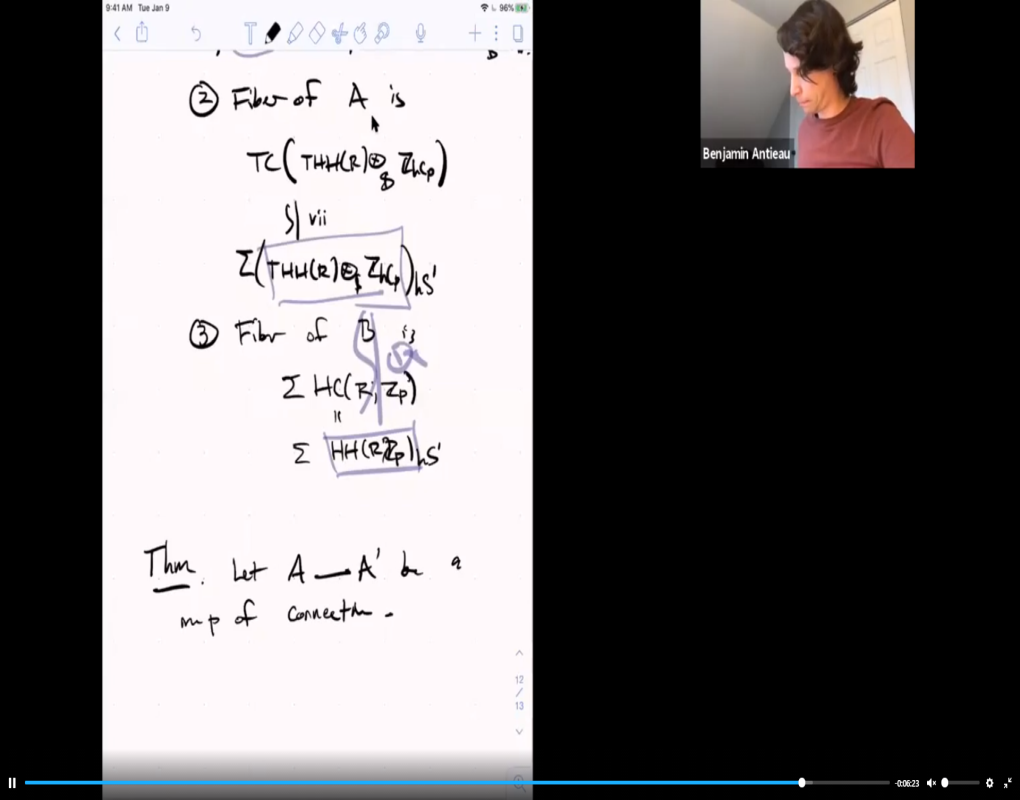
The Beilinson fiber square
Presenter
March 23, 2020
Keywords:
- p-adic K-theory
- cyclic homology
- deformation of algebraic cycles
- motivic cohomology
MSC:
- 14F30
- 14F40
- 19D55
- 19E15
Abstract
If R is an associative ring satisfying some mild technical conditions, Beilinson constructs a fiber sequence of spectra identifying the fiber of the map \lim_n K(R/p^n)\rightarrow K(R/p) with a suspension of the ordinary cyclic homology of R, all up to p-completion followed by inverting p. Joint work with Akhil Mathew, Matthew Morrow, and Thomas Nikolaus provides a new proof of this fact using recent advances in the theory of cyclotomic spectra due to Nikolaus and Scholze. I will explain the motivation for this fiber sequence, which has to do with the infinitesimal part of the p-adic variational Hodge conjecture, and then I will give a construction of the fiber sequence and of a more general fiber square.