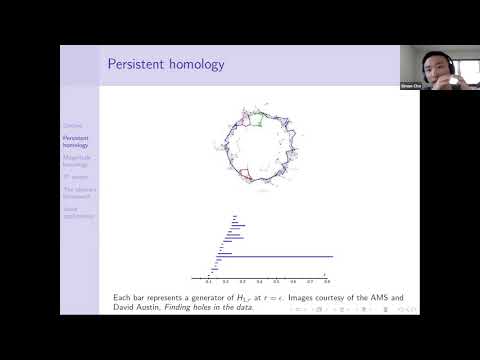
Motivated by thematic similarities between persistent homology and magnitude homology, we describe a simplicial construction associated to a metric space. This construction is determined by (apart from the metric space itself) a choice of two parameters, which we may take to be real-valued. Applying homology pointwise, we get persistent homology on one end of the possible choices of parameters, and magnitude homology on the opposite end. Time permitting, we describe some modest applications of this perspective.