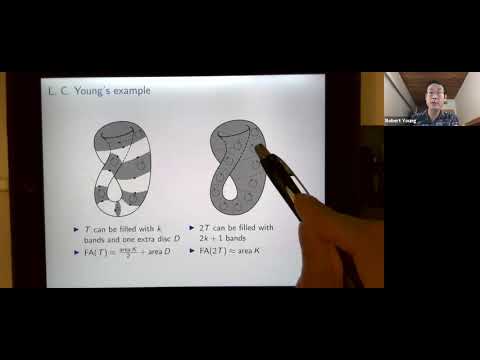
Filling a curve with an oriented surface can sometimes be "cheaper by the dozen". For example, L. C. Young constructed a smooth curve drawn on a projective plane in $\mathbb R^n$ which is only about 1.5 times as hard to fill twice as it is to fill once and asked whether this ratio can be bounded below. This phenomenon is based on the nonorientability of the projective plane; we will define a new invariant that measures how nonorientable a manifold is and bound it by decomposing surfaces in $\mathbb R^n$ into uniformly rectifiable pieces.