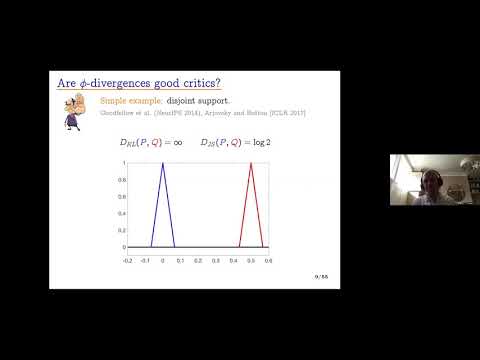
I will introduce Generalized Energy Based Models (GEBM) for generative modelling. These models combine two trained components: a base distribution (generally an implicit model), which can learn the support of data with low intrinsic dimension in a high dimensional space; and an energy function, to refine the probability mass on the learned support. Both the energy function and base jointly constitute the final model, unlike GANs, which retain only the base distribution (the "generator"). In particular, while the energy function is analogous to the GAN critic function, it is not discarded after training.GEBMs are trained by alternating between learning the energy and the base. Both training stages are well-defined: the energy is learned by maximising a generalized likelihood, and the resulting energy-based loss provides informative gradients for learning the base. Samples from the posterior on the latent space of the trained model can be obtained via MCMC, thus finding regions in this space that produce better quality samples. Empirically, the GEBM samples on image-generation tasks are of much better quality than those from the learned generator alone, indicating that all else being equal, the GEBM will outperform a GAN of the same complexity. GEBMs also return state-of-the-art performance on density modelling tasks, and when using base measures with an explicit form.