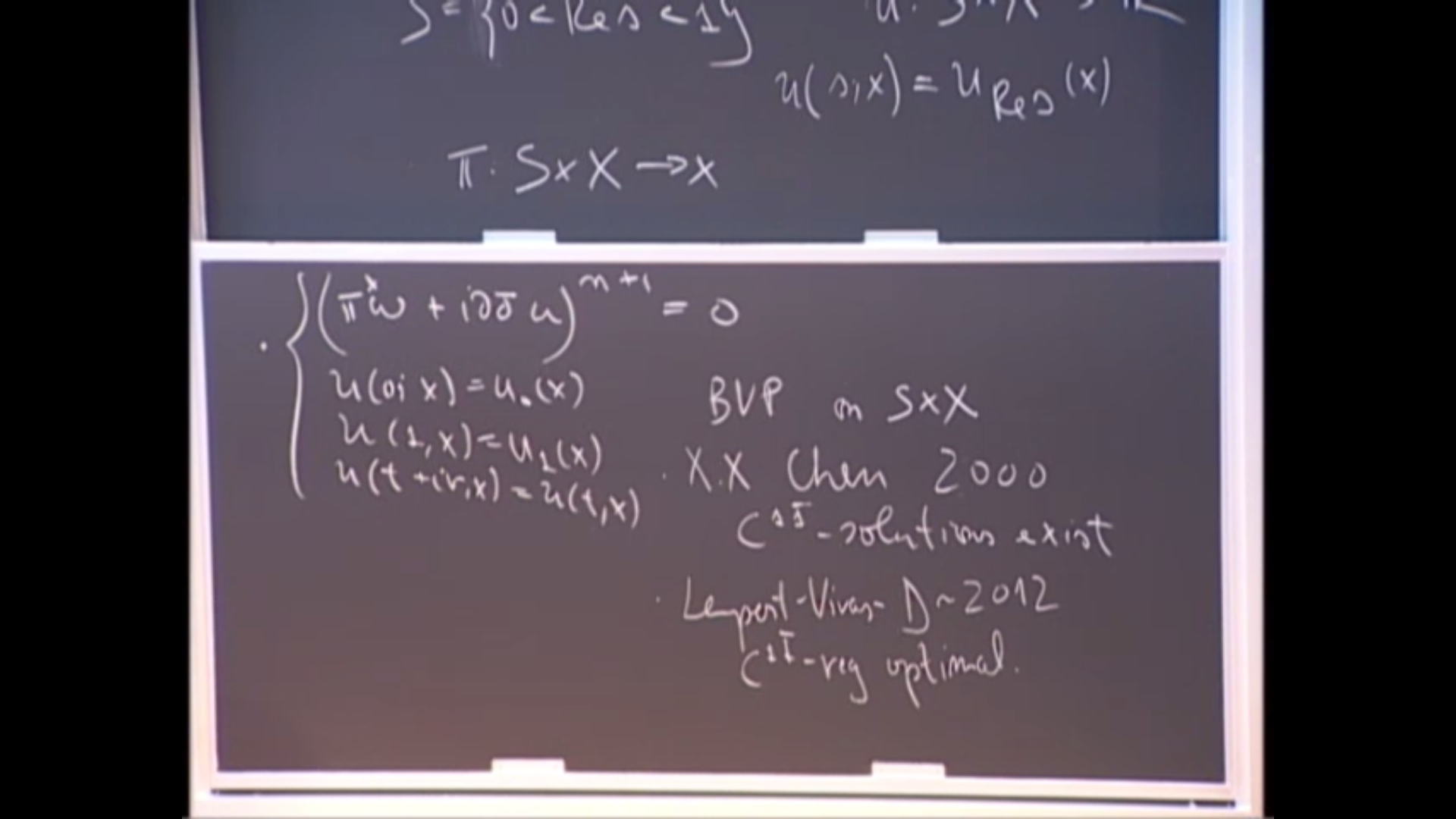we introduce the L^p Mabuchi-Finsler structures on the space of Kahler metrics and present the resulting path length geometries. All the metric completions are geodesic metric spaces that can be characterized using elements of finite energy pluripotential theory and we focus on three particular cases of interest. Using convexity in the L^\infty geometry, one may be able to obtain C^0 estimates for variational PDE problems arising in Kahler geometry. The L^2 geometry is non-positively curved and seems to be the ideal context to study metric properties of gradient flows of various convex functionals, including the Calabi flow and the J-flow. The L^1 geometry enjoys a compactness property and has metric growth prescribed by the J functional, making it a useful tool in the study of energy properness questions, leading to the recent resolution of Tian's related conjectures.