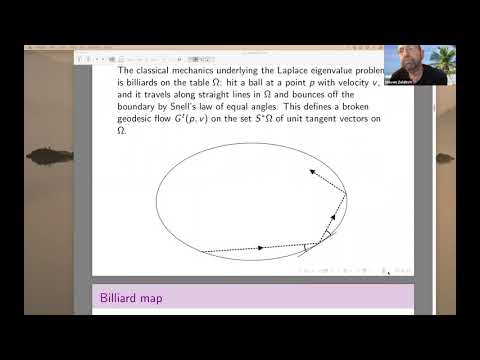
Ellipses of small eccentricity are determined by their Dirichlet (or, Neumann) spectra
Presenter
April 28, 2020
Abstract
In 1965, M. Kac proved that discs were uniquely determined by their Dirichlet (or, Neumann) spectra. Until recently, disks were the only smooth plane domains known to be determined by their eigenvalues. Recently, H. Hezari and I proved that ellipses of small eccentricity are also determined uniquely by their Dirichlet (or, Neumann) spectra. The proof uses recent results of Avila, de Simoi, and Kaloshin, proving that nearly circular plane domains with rationally integrable billiards must be ellipses. It also uses a ``bounce decomposition'' for the wave trace, representing the wave trace as a sum of q-bounce oscillatory integrals. It is shown that for nearly circular domains, each is a spectral invariant and that the ellipse is uniquely determined by its q-bounce invariants.