Nonlinear inviscid damping in 2D Euler
Presenter
October 18, 2013
Keywords:
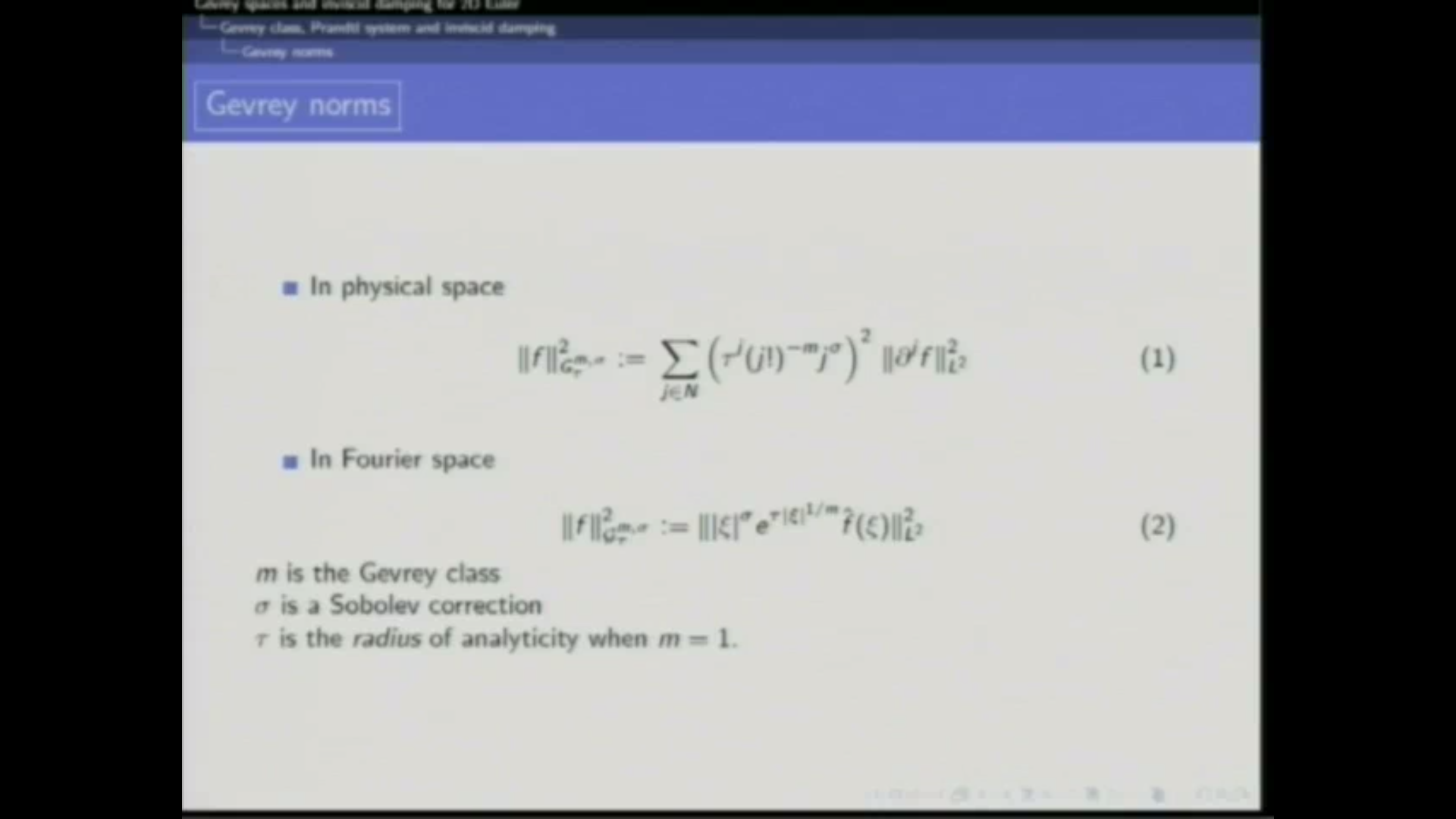
- inviscid limit
- dampened PDE
- Euler equations
- energy estimates
- Couette flow
- Landau damping
- functional analysis and PDE
MSC:
- 35Q35
- 35Q74
- 35Q86
- 35Q93
- 76Dxx
- 35Q31
Abstract
We prove the global asymptotic stability of shear flows close to planar Couette flow in the 2D incompressible Euler equations. Specifically, given an initial perturbation of the Couette flow which is small in a suitable regularity class we show that the velocity converges strongly in L2 to another shear flow which is not far from Couette. This strong convergence is usually referred to as "inviscid damping" and is roughly analogous to Landau damping in the Vlasov Poisson equations. This is a joint work with Jacob Bedrossioan