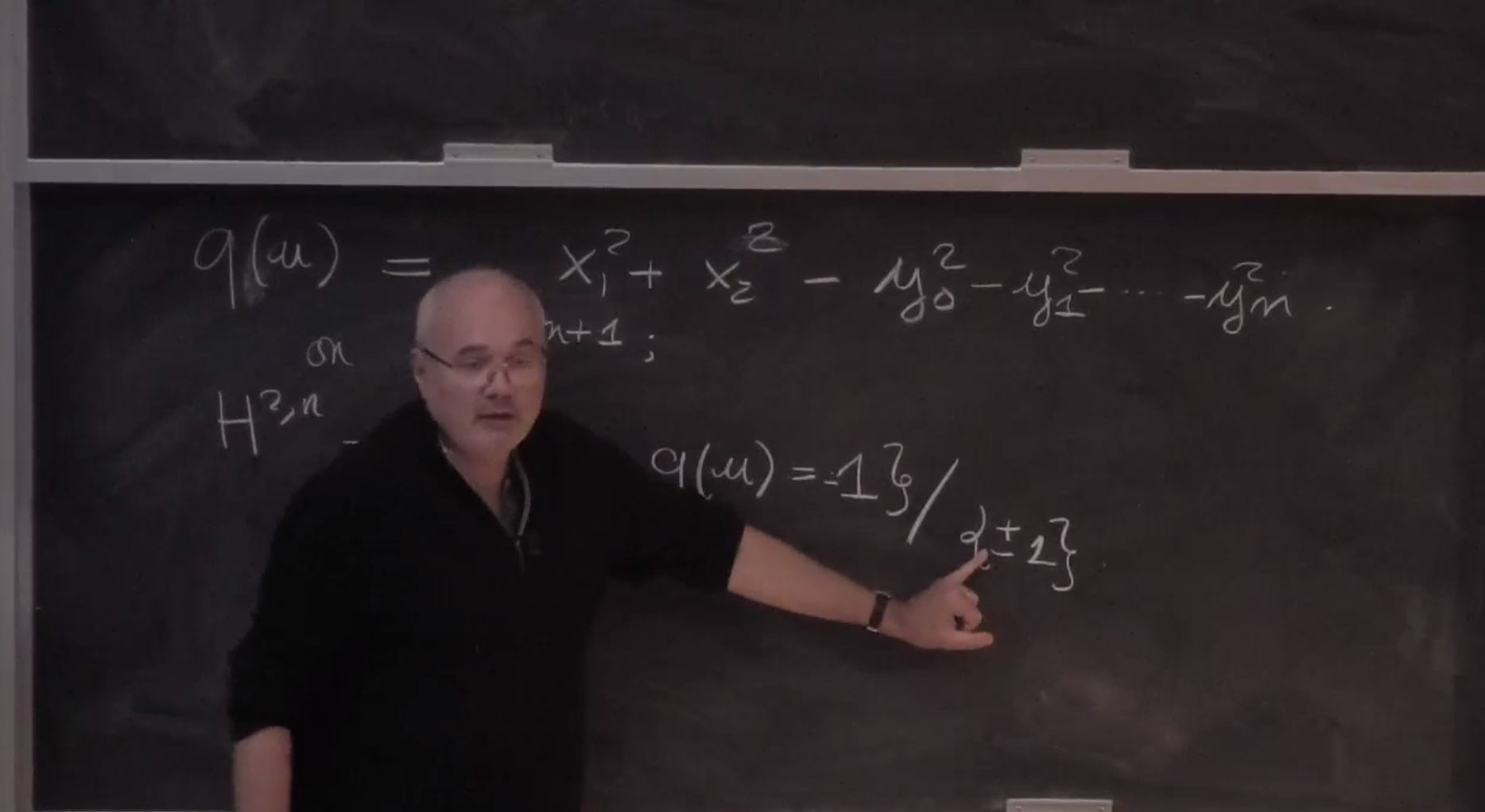Maximal surfaces in pseudo-hyperbolic spaces of rank 2
Presenter
November 21, 2019
Abstract
In this joint work with Jérémy Toulisse and Mike Wolf, we prove the existence (and discuss the uniqueness) of maximal surfaces in the pseudo-hyperbolic space $H_{2,n}$
of signature (2,n) with a prescribed quasi-symmetric boundary at infinity.
No knowledge of Lorentzian geometry will be assumed. We will mainly discuss the notion of quasi-symmetric curves in the boundary at infinity of $H_{2,n}$, boundary known as the EInstein universe