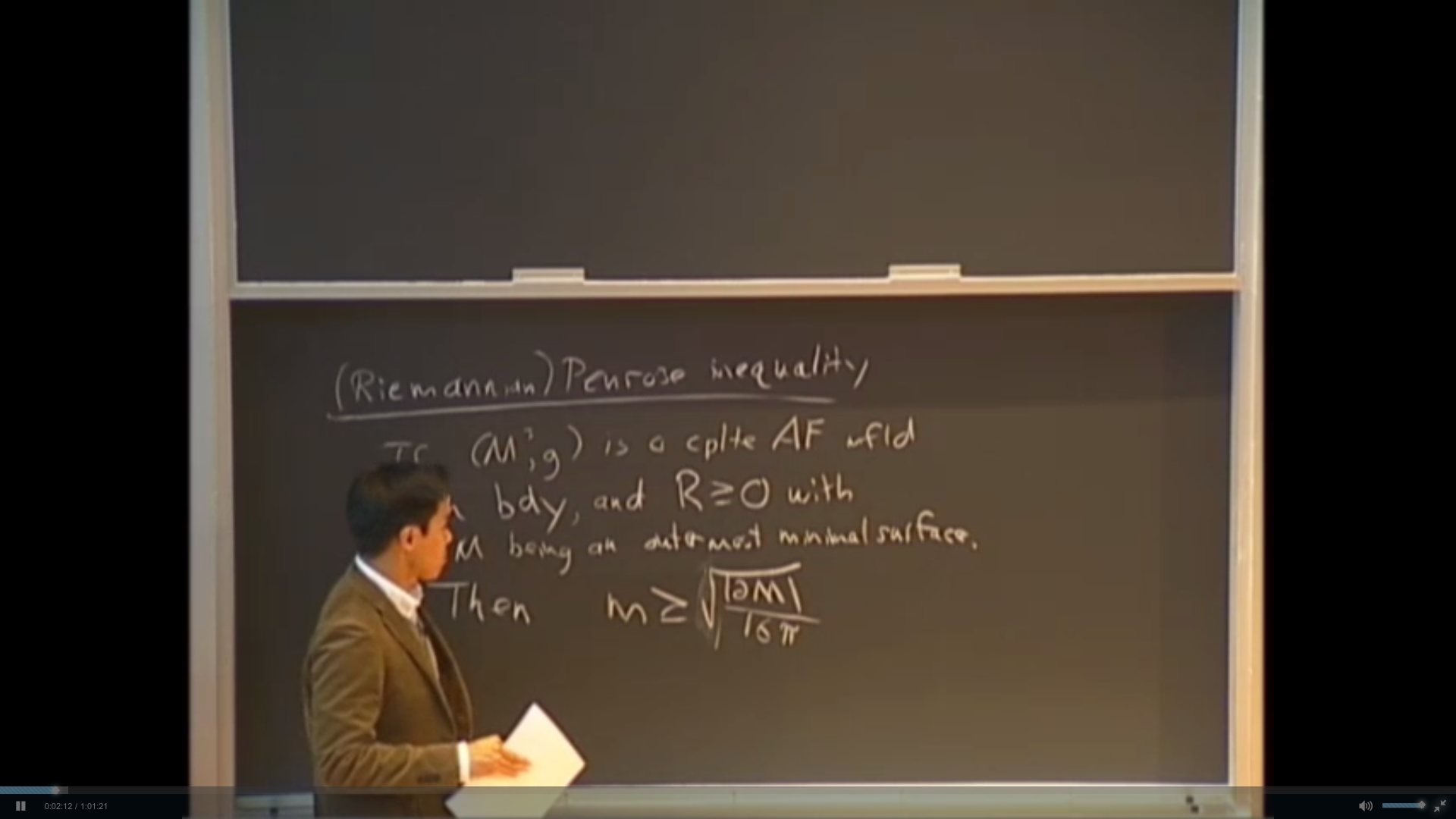The Penrose inequality for asymptotically locally hyperbolic spaces with nonpositive mass
Presenter
November 22, 2013
Keywords:
- asymptotic geometry
- Lorentzian geometry
- Penrose diagram
- mathematical general relativity
- positive energy conditions
- wave equations
- wave
- wave mechanics
MSC:
- 83Cxx
- 83-xx
- 83C05
- 83C22
- 83C20
- 83C40
- 83C60
- 83Fxx
Abstract
In the asymptotically locally hyperbolic setting it is possible to have metrics with scalar curvature at least -6 and negative mass when the genus of the conformal boundary at infinity is positive. Using inverse mean curvature flow, we prove a Penrose inequality for these negative mass metrics. The motivation comes from a previous result of P. Chrusciel and W. Simon, which states that the Penrose inequality we prove implies a static uniqueness theorem for negative mass Kottler metrics.